こんにちは、毛糸です。
会計は企業の活動を財務諸表という成績表として表現するためのルールであり、「複式簿記」の規則に従って財務諸表が作られます。
簿記を学習するうえでは、簿記3級のような資格にチャレンジしたことがあるかと思いますが、そこでは複式簿記の規則が問われます。
今回は、そんな複式簿記の、ちょっと変わった考え方についてお話します。
本記事でお話するのは、複式簿記を「行列」で表す「行列簿記」という手法です。
行列簿記とはなにか
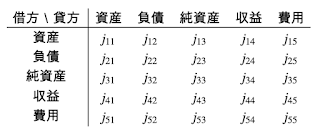
行列簿記とは、複式簿記の貸方と借方を、行列の行と列に対応させた表現方法です。
具体例を挙げましょう。
期中において、以下の取引があったとします。
①減価償却(直接法)
②債務免除
③配当
期中の仕訳は、借方に記入される勘定を列方向に、貸方に記入される勘定を行方向に置いた行列として表します。
具体的には①
\hline 資産&0&0&0&0&0\\
負債&0&0&0&0&0\\
純資産&0&0&0&0&0\\
収益&0&0&0&0&0\\
費用&x&0&0&0&0\\ \end{array} \]
②
\hline 資産&0&0&0&0&0\\
負債&0&0&0&y&0\\
純資産&0&0&0&0&0\\
収益&0&0&0&0&0\\
費用&0&0&0&0&0\\ \end{array} \]
③
\hline 資産&0&0&0&0&0\\
負債&0&0&0&0&0\\
純資産&z&0&0&0&0\\
収益&0&0&0&0&0\\
費用&0&0&0&0&0\\ \end{array} \]
借方と貸方を行列で表現することで、複式簿記を2次元的に捉えることが可能になるのです。
なお行・列を
- 貸・借に対応付ける行列簿記の方法を貸行借列法(たいぎょうしゃくれつほう)
- 借・貸に対応付ける行列簿記の方法を借行貸列法(しゃくぎょうたいれつほう)
と使い分けることもあるようです。これらの使い分けに関しては、以下の参考文献の第6章「DBMSと複式簿記」をご覧ください。
行列簿記の先行研究
「借方と貸方を行列で表現する」という考え方は実に明快で、複式簿記を数学の世界に持ってくるための方法としてはよく出来ているように思えます。
借方貸方という複式簿記の独自規則から離れ、行列によって仕訳や試算表を表現できるので、コンピュータでのデータの管理や分析にも役立つことが期待されます。
実際、この「複式簿記の行列表現」=「行列簿記」は以前から研究されており、記帳実務の効率化はもちろん、管理会計や企業価値評価にも応用できると考えられています。
上述の『行列簿記の現代的意義』は行列簿記が持つアドバンデージや、歴史や、データベースとの関係について詳しく論じられたテキストであり、行列簿記を学ぼうとするひとがまず手に取るべき本と言えるでしょう。
また、ネットからアクセス可能な論文『行列簿記による企業分析』には行列簿記の概念や方法論がよくまとまっており有用です。
行列簿記の性質
行列簿記は仕訳の整理に有用であり、行列操作による勘定の締切や繰越も行えるなど、会計システムとしての性格を備えています。
仕訳や試算表は、勘定数×勘定数の正方行列の各要素に正数を配置して作成されます。
行の和、列の和はそれぞれ、各勘定の借方残高、貸方残高に対応します。
仕訳を表す行列に集計ベクトル(全要素が1のベクトル)を左・右から乗じることで、簡単に借方・貸方残高を計算できます。
また、仕訳や試算表を行列=線形空間上の点として表すことで、コンピュータでの処理や演算が簡単になります。
任意の仕訳は行列表示することができ、仕訳の積み重ねが試算表になるという関係も、行列の和として自然に定義できます。
このような操作性に基づき、行列簿記は数学的な分析手法、とくにリニアプログラミング(線形計画法)と相性がいいとされています。
リニアプログラミングによって与えられた行列から将来予測を行うことができるなど、現代においても有用性を見出すことができます。
行列簿記の限界
複式簿記を行列形式で表現することにより、仕訳の積み上げや残高の計算が簡単になりそうだというメリットが考えられます。
一方で、勘定科目の数だけ次元を持つ行列を考えることになるので、通常はとても「大きな」行列が作られることが想定されます。取引全体を見渡せるという行列簿記の良さの裏返しでもありますが、帳票が大きくなりすぎることのメリットとどこまで釣り合うのかは疑問符が付きます。
行列簿記は仕訳の借方貸方を2次元配列で表現し直したに過ぎず、行列表現された仕訳に対して処理(行列式を計算したり、逆仕訳を考えるなど)をすると、その処理そのものと処理されたアウトプットに、会計的な意味を与えられない、という欠点があります。
せっかく複式簿記に行列という数学的な姿を与えても、数学の世界で当然に行える議論の結果を、再び会計の世界に引き戻すことが難しいのです。
→上記の点に関して、行列式や逆行列を使って取引の詳細を把握したり、原価計算における配賦問題を考えるなど、帳簿を行列として表すことには大きなメリットがあるようです。
詳細は『行列簿記の現代的意義』のほか、田中『行列簿記の有用性と限界(Ⅱ完)』をご覧ください。
ただし、大きなサイズの行列を扱ううえ、その行列の多くの成分は0であることから、逆行列などの計算には大きな困難があることが予想されます。
成分に0が多い行列を疎行列とかスパース行列といいます。スパース性を持つ行列に関する操作に関しては、工学分野で多くの研究があるので、参考になるでしょう。
行列簿記から簿記代数へ
行列簿記は仕訳の貸借を行列に対応付ける素朴なアイデアと考えがちですが、単なる表現の違い以上の大きな重要性があります。
ただ、個人的な印象として、行列を含むより抽象的な数学概念との結びつきを理解しにくい部分があります。
もし複式簿記の性質や構造を、抽象的な数学概念と結びつけることができれば、数学における発見を簿記の研究に「輸入」することが可能になります。
複式簿記を抽象的な数学の言葉で語ることはできないのか。
そう悩んだ末に見つけたのが以下の書籍です。
この本は複式簿記を代数の言葉で表し、複式簿記の本質が「自由加群」であることを明らかにし、そこから議論を組み立てている、異色の会計学のテキストです。
シリーズ【君の知らない複式簿記】では、こうした複式簿記の数学的考察をまとめています。
SNSでご意見や応援をお寄せいただければ、大変嬉しく思います。