こんにちは、毛糸です。
私は【投信定点観測】と題して、投資を行っています。
参考記事:【投信定点観測】インデックス投資信託8つ・ロボアドバイザー2つ・アクティブファンド3つにドルコスト平均法で積立投資してみる
しかし、私のように投資をしていない人でも、日本人はほぼ全員、金融リスクをとっている、ということをご存知でしょうか。
それは「年金」です。
私たちが加入している国民年金は、年金積立金管理運用独立行政法人(GPIF)という機関によって運用されており、株や債券といったリスク資産に投資が行われています。
リスク資産に投資が行われているということは、ある程度のリターンを期待して、リスクをとっているということです。
今回は、私たちの年金がどれくらいのリスクを負い、リターンを求めているのかを、プログラミング言語Rを用いて計算してみたいと思います。
統計プログラミング言語Rと、オンラインでの利用
統計プログラミング言語Rは、データサイエンスで頻繁に用いられるプログラミング言語です。
統計解析や計算を簡単に行うことができ、計算機としても使えます。
本記事ではプログラミング言語Rを用いて、年金ポートフォリオのリターンとリスクを計算します。
Rを使うには、本来RというソフトウェアをPCにインストールする必要がありますが、今回はちょっとした計算に使うのみなので、ブラウザ上で完結するR onlineを利用します。
参考記事:ブラウザ上でRプログラミング(R online、Rオンラインを使う方法)
R onlineのサイト(リンク)でコードを打ち込めば、すぐにRによる計算が実行できます。
試しにサイト上で
1+1
と入力し、[Run it]してみると、すぐに下の方に計算結果が表示されます。
以下、このR onlineを使って、年金ポートフォリオのリターンとリスクを計算します。
すでに打ち込んである内容は、すべて削除して構いません。
GPIFの基本ポートフォリオ
年金はリスク資産に投資を行って運用されています。
年金運用を行っている年金積立金管理運用独立行政法人(GPIF)は、リスク資産への投資に関して、「基本ポートフォリオの考え方」(外部リンク)という指針を示しています。
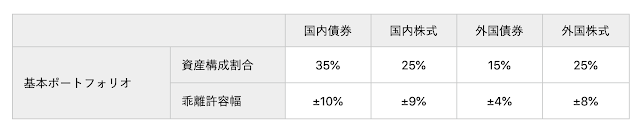
GPIFは「基本ポートフォリオの考え方」のなかで、年金ポートフォリオとして
- 国内債券
- 国内株式
- 外国債券
- 外国株式
(出典:https://www.gpif.go.jp/gpif/portfolio.html)
早速、この基本ポートフォリオをRでコーディングしてみましょう、以下のように入力して、[Run it]してください。
#基本ポートフォリオ(各資産クラスのウエイト) weight<-c(0.35,0.25,0.15,0.25,0)
ここではweightという変数に、各資産クラスのウエイトを代入しています。c()というのは、数字を並べてひとくくりにします、というときに使う決まり文句です。
5つの数字はそれぞれ、図の中の資産構成割合を示しています(最後の0は短期資産ですが、表にはありません)。
資産構成割合をすべて足すと1(100%)になることが確認できます。
#足すと1になることを確認 (sum(weight))
基本ポートフォリオのリターン
これら期待リターンをもちいて、年金ポートフォリオのリターンを計算してみます。
まず、各資産の期待リターンをRでコーディングしてみましょう、以下のように入力して、[Run it]してください。
#各資産クラスの期待リターン(名目、経済中位) mu<-c(2.6/100, 6.0/100, 3.7/100, 6.4/100, 1.1/100)
金融工学では期待リターンを\( \mu\)(ミュー、mu)と表すことが多いので、muとしています。
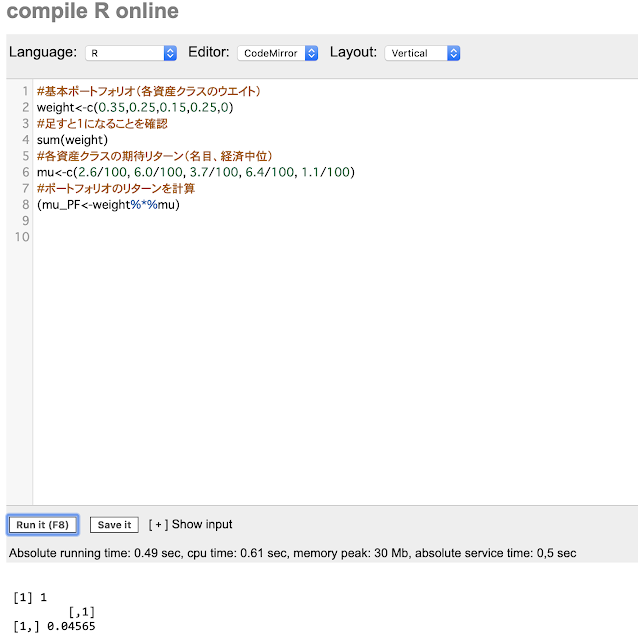
基本ポートフォリオのリターンは、各資産クラスのリターンに、前述の基本ポートフォリオのウエイトをかけることで求められます。
#ポートフォリオのリターンを計算 (mu_PF<-weight%*%mu)
テクニカルな話ですが、weightとmuはどちらも「ベクトル」なので、その掛け算には%*%という記号を使います。
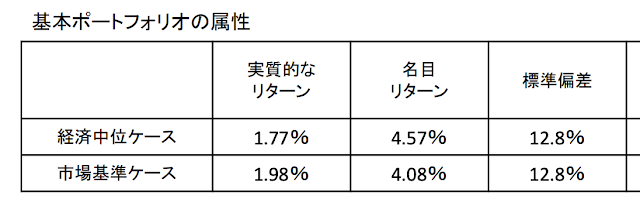
結果は0.04565(4.57%)となりました。これが年金の基本ポートフォリオの期待リターンです。
「【参考資料】年金積立金管理運用独立行政法人の中期計画(基本ポートフォリオ)の変更」(PDFリンク)の9ページ目に、これと全く同じ数字が記載されています。
基本ポートフォリオのリスク
[Run it]してください。
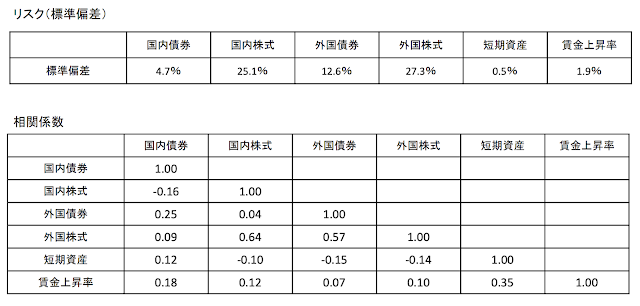
#各資産クラスの分散(標準偏差の2乗) sigma<-c(0.047,0.251,0.126,0.273,0.005) #相関行列 Rho<-rbind( c(1,-0.16,0.25,0.09,0.12), c(-0.16,1,0.04,0.64,-0.1), c(0.25,0.04,1,0.57,0.15), c(0.09,0.64,0.57,1,-0.14), c(0.12,-0.1,-0.15,-0.14,1))
rbind()というのは、c()でまとめた数値(ベクトル)を縦に並べる、という意味の関数です。
これら情報だけでは、基本ポートフォリオのリスクは計算できません。
基本ポートフォリオのリスクを計算する前に、各資産クラスの分散と相関行列から、分散共分散行列というものを作る必要があります。
以下のように入力したら、[Run it]してください。
#分散対角行列 sigma_diag<-diag(sigma) #分散共分散行列 Sigma<-sigma_diag%*%Rho%*%sigma_diag
分散共分散行列にウエイトをかけることで、基本ポートフォリオの分散を計算することが出来ます。
なぜこういう計算になるのかという疑問がわきますが、「線形代数」という数学を勉強するとわかるようになります(記事の末尾に参考文献を挙げます)。
R onlineに以下のように入力したら、[Run it]してください。
#ポートフォリオの分散 Var_PF<-weight%*%Sigma%*%weight
分散の2乗根(ルートのこと、0.5乗も同じ)が標準偏差(リスク)になります。
#ポートフォリオのリスク(標準偏差) (sigma_PF<-Var_PF^0.5)
結果は0.1276…(12.8%)となりました。これが年金の基本ポートフォリオのリスクです。
「【参考資料】年金積立金管理運用独立行政法人の中期計画(基本ポートフォリオ)の変更」(PDFリンク)の9ページ目に、これと全く同じ数字が記載されています。
まとめ
本記事では、年金運用の基本ポートフォリオのウエイトと期待リターン、分散等の情報から、年金ポートフォリオのリターンとリスクを計算しました。
私たちの年金の原資となっている資産は、リスク12.8%を追うことで、期待リターン4.57%の獲得を目指しています。
こうした分析は、統計や数学を少し勉強すれば簡単に行なえますので、是非ご自分でも興味を深めてみてください。
参考文献等
投資分析に必要な数学は、高校数学が基本となっていますので、復習してみることをおすすめします。
一歩進んだ投資分析には、行列や線形代数の知識が必要になりますが、金融データ分析を扱うテキストではそういった分野を解説してくれているものもあります。