長期投資は【安全ではない】ことをシミュレーションで証明する

こんにちは、毛糸です。

「長期投資は安全」というイメージを抱いていませんか？

全国銀行協会のサイト（リンク）でも、長期投資の安全性に関して以下のように書いてあります。

一時的に価格が下がっても、長い目で見れば価格が上がることもあるため、長く保有すればするほど、リスクを軽減する効果があるといわれています。

しかし、この主張は極めて誤解しやすいもので、実際にはむしろ、投資収益のリスクは長期になればなるほど大きくなります。

本記事では「投資シミュレーションプログラム」を用いて、長期投資がリスクを高めることを証明します。
参考記事：>>「投資シミュレーションプログラム」サマリー

投資の「リスク」の定義

投資におけるリスクとは、投資収益の期待値からのブレを指すのが一般的です。

もう少し踏み込んで言えば、そのブレを測る尺度が、標準偏差や分散という統計量です。

投資において「リスクが高い」とは、将来の（額もしくは率ベースの）投資収益の標準偏差が高い、ということを意味します。

この意味において、投資が長期になればなるほど、リスクは高くなります。

つまり、他の条件を一定とすれば、短期と長期の投資収益は、後者のほうが高い標準偏差を持つということです。

本記事ではこのことを「投資シミュレーションプログラム」を用いて示します。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”ウォール街のランダムウォーカー株式投資の不滅の真理”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51j3XxuLcML.jpg”,”/51L5VguO16L.jpg”,”/51pXH1cT26L.jpg”,”/51qzhDA8N8L.jpg”,”/516KF7nD4ML.jpg”,”/51RqxJ5YdzL.jpg”,”/41Z4TQLguaL.jpg”,”/41RDCEkVSWL.jpg”,”/51ZC6wiROQL.jpg”,”/416UAK2gjbL.jpg”,”/51COLQfOYZL.jpg”,”/41wAkIpxalL.jpg”,”/517pu9qvoaL.jpg”,”/51Qd00xstPL.jpg”,”/41a6WwcjPUL.jpg”,”/41whOykxo9L.jpg”,”/51ZYk6jqWTL.jpg”,”/51JXyzvOypL.jpg”,”/51Cx1OLwZwL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%82%A6%E3%82%A9%E3%83%BC%E3%83%AB%E8%A1%97%E3%81%AE%E3%83%A9%E3%83%B3%E3%83%80%E3%83%A0%E3%83%BB%E3%82%A6%E3%82%A9%E3%83%BC%E3%82%AB%E3%83%BC%E3%80%88%E5%8E%9F%E8%91%97%E7%AC%AC11%E7%89%88%E3%80%89-%E2%80%95%E6%A0%AA%E5%BC%8F%E6%8A%95%E8%B3%87%E3%81%AE%E4%B8%8D%E6%BB%85%E3%81%AE%E7%9C%9F%E7%90%86-%E3%83%90%E3%83%BC%E3%83%88%E3%83%B3%E3%83%BB%E3%83%9E%E3%83%AB%E3%82%AD%E3%83%BC%E3%83%AB/dp/4532356873″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”azSuX”});

投資シミュレーションプログラム

「投資シミュレーションプログラム」は、確率論に基づくモンテカルロ・シミュレーションという手法を用いて、投資収益の将来予測をするプログラムです。
参考記事：>>「投資シミュレーションプログラム」サマリー

モンテカルロ・シミュレーションとは、コンピュータによって乱数を発生させ、将来を確率的にシミュレートし、大数の法則によって将来の期待値を算定する手法です。

「投資シミュレーションプログラム」を使えば、投資の期待リターンとリスクと投資期間を入力することで、将来の資産額を計算することが出来ます。

長期投資でリスクは低減されない

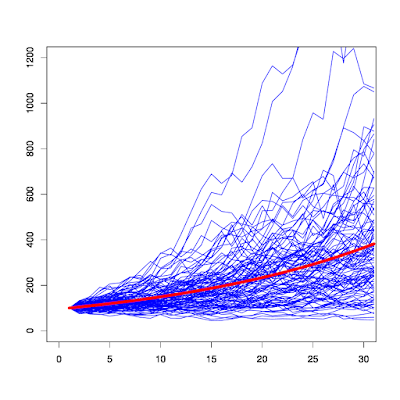
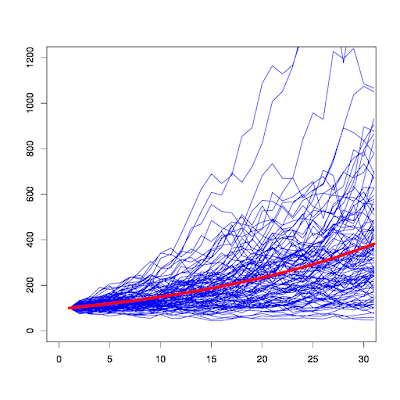
今回行うシミュレーションは、投資対象をFXとした場合（期待リターン0％、リスク10％と仮定）と、インデックス投信に分散投資した場合（期待リターン4.57%、リスク12.8％）の2つのケースについて、1年・10年・30年の各投資期間で、将来時点で確定する投資収益の期待値とリスクを計算してみます。

インデックス投信に分散投資、といってもアセット・アロケーションは無限にありますが、ここでは日本の年金運用の基本ポートフォリオと同じ資産配分で行うものと仮定します。

シミュレーション結果は以下のとおりです。

FX（期待リターン0％、リスク10％）に投資した場合

1年後

10年後

30年後

#FX
#投資年数（自由入力）
Year<-1
#シミュレーション回数（自由入力、多いほど正確だが時間がかかる）
sample<-10000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)
#初期投資額を入力（自由入力）
initial<-100
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#期待リターン（期待収益率μ、自由入力）
mu<-0/100
#リスク（標準偏差σ、自由入力）
sigma<-10/100
#シミュレーション開始
set.seed(123)
#sampleの計算は明示せずベクトル化
for ( t in 1:Year){
    #今年の資産額=前年の資産額*(1+収益率)
    A[,t+1]<-A[,t]*(1+rnorm(sample,mu,sigma))
}
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の平均は",mean(A[,Year+1]),"万円")
paste(Year,"年後の累積リターンの平均は",(mean(A[,Year+1])/initial-1)*100,"%")
paste(Year,"年後の累積リターンの標準偏差は",sd(A[,Year+1])/initial*100,"%")
paste(Year,"年間の1年あたり　平均収益率は",((mean(A[,Year+1])/initial)^(1/Year)-1)*100,"%")

#インデックス
#投資年数（自由入力）
Year<-1
#シミュレーション回数（自由入力、多いほど正確だが時間がかかる）
sample<-10000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)
#初期投資額を入力（自由入力）
initial<-100
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#期待リターン（期待収益率μ、自由入力）
mu<-４．５７/100
#リスク（標準偏差σ、自由入力）
sigma<-12.8/100
#シミュレーション開始
set.seed(123)
#sampleの計算は明示せずベクトル化
for ( t in 1:Year){
    #今年の資産額=前年の資産額*(1+収益率)
    A[,t+1]<-A[,t]*(1+rnorm(sample,mu,sigma))
}
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の平均は",mean(A[,Year+1]),"万円")
paste(Year,"年後の累積リターンの平均は",(mean(A[,Year+1])/initial-1)*100,"%")
paste(Year,"年後の累積リターンの標準偏差は",sd(A[,Year+1])/initial*100,"%")
paste(Year,"年間の1年あたり　平均収益率は",((mean(A[,Year+1])/initial)^(1/Year)-1)*100,"%")

まとめ

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”[参考文献]ファイナンスのためのRプログラミング証券投資理論の実践に向けて”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/41UrHrQ9vlL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%8A%E3%83%B3%E3%82%B9%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AER%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E2%80%95%E8%A8%BC%E5%88%B8%E6%8A%95%E8%B3%87%E7%90%86%E8%AB%96%E3%81%AE%E5%AE%9F%E8%B7%B5%E3%81%AB%E5%90%91%E3%81%91%E3%81%A6%E2%80%95-%E5%A4%A7%E5%B4%8E-%E7%A7%80%E4%B8%80/dp/4320110447″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”GI2A5″});