こんにちは、毛糸です。
日本の年金制度に対する不透明感から、資産運用の必要性を感じている人も増えてきていることと思います。
資産運用の「王道」として挙げられるのが、投資信託などを毎月定額で積み立て購入する手法「ドルコスト平均法」です。
ドルコスト平均法は初心者でも実施できる効果的な投資手法として紹介されることも多いですが、実はその有用性については評価が分かれています。
本記事ではドルコスト平均法の有効性を検証することが難しい2つの理由を解説します。
ドルコスト平均法とは
ドルコスト平均法は投資手法の一つであり、決まった期間ごと（たとえば一ヶ月ごと）に一定の金額を投資することを指します。
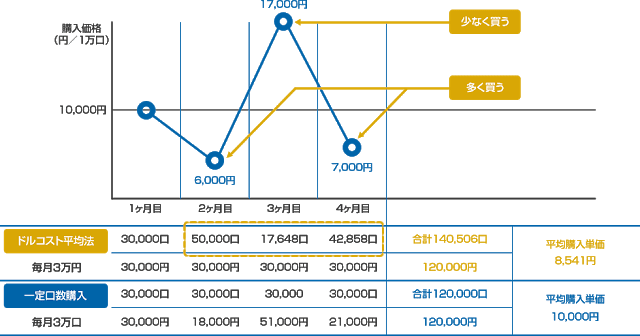
ドルコスト平均法は投資の平均買い付け価格を下げる効果があるとされています。
ドルコスト平均法の考え方は単純で、手軽に行える投資手法であり、上記のような「効果」があるとされているため、人気の手法です。
しかし、ドルコスト平均法が投資手法として優れているのかというのは、学術的には肯定的な意見も否定的な意見もあり、科学的に立証された方法ではありません。
資産運用の初心者におすすめの入門書『難しいことはわかりませんが、お金の増やし方を教えてください！』には、ドルコスト平均法について、
三流ファイナンシャルプランナーが書いたんじゃない？
早めに買ってお金に働いてもらう期間が長いほうが、現時点の判断としては正しい。
と書かれており、ドルコスト平均法に否定的です。
このように、専門家の間でもドルコスト平均法の有効性については判断が分かれています。
以下ではなぜドルコスト平均法の検証が難しいのか、2つの理由を挙げます。
データ期間に依存する
ドルコスト平均法に関する設例の多くは、資産価格が上げ下げを繰り返すようなケースがほとんどです。
こういうケースにおいては、ドルコスト平均法によって、買い付け単価の平均は小さく抑えられます。
出典：三井住友DSアセットマネジメントhttps://www.daiwasbi.co.jp/fundcollege/investment/about/index4.html
しかし、これはあくまで「そういう相場だから有利だった」という話で、これからも上げ下げを繰り返すような相場になるとは限りません。
時には今を「底」として右肩上がりで資産価格が上昇する場合もあり、そのときは当初一括購入するのが、最も買い付け単価を安くする方法です。
このように、ドルコスト平均法の検証につかうデータ次第では、ドルコスト平均法が有利とも不利とも言えることになります。
したがって、特定期間のデータに依拠したドルコスト平均法の分析は説得力にかけるものがほとんどです。
データ期間に依存しない一般的なケースでの分析が難しいことが、ドルコスト平均法の分析を難しくする要因のひとつとなっています。
確率論の問題として扱いづらい
投資を確率論の立場から検証するのがファイナンス理論です。
ブラック・ショールズ式を厳密に証明しノーベル賞を受賞したロバート・マートンも、確率論に基づく最適ポートフォリオの研究をしています。
ファイナンス理論において投資を分析するのは今やメジャーとなっていますが、しかし、ドルコスト平均法は標準的なファイナンス理論とあまり相性がありません。
標準的なファイナンス理論では、資産価格が対数正規分布に従うと仮定されます。
参考記事>>年金のリスクとリターンを統計プログラミング言語Rで計算してみた
参考記事>>年金のリスクとリターンを統計プログラミング言語Rで計算してみた
ドルコスト平均法は、異なる時点で一定金額を買い付ける手法であり、その際の購入量は一定金額÷資産価格で求められます。
計算によって、この購入量もまた、対数正規分布に従うことがわかります。
数式で書くと、時点\( t\)において資産価格が\( S_t\)だったときに、一定額\( A\)を投資したときの購入量\(Q_t \)は、以下のように表すことができ、これは対数正規分布に従います。
\[ \begin{split} Q_t=\frac{A }{S_t }=\frac{ A}{ S_0}e^{-(\mu-\frac{ 1}{ 2}\sigma^2)t-\sigma W_t}\end{split} \]
ただし、\( \mu\)は資産の期待リターン、\( \sigma\)はリスク、\( W_t\)は正規分布に従う確率変数です。
さて、ドルコスト平均法によった場合、購入は何度かに分かれて行われるため、最終的な投資量は各回の購入量の和、すなわち対数正規分布の和になります。
対数正規分布の和は、数式で簡潔に表現することができません。
参考記事>>対数正規分布の和、幾何ブラウン運動の和、リスク資産ポートフォリオ
参考記事>>対数正規分布の和、幾何ブラウン運動の和、リスク資産ポートフォリオ
正規分布であれば、正規分布の和は再び正規分布になり、簡潔に表現することができますが、対数正規分布の和は扱いやすい確率分布にはなりません。
したがって、確率論を使ってドルコスト平均法の定量的な議論を行うのは難しくなります。
もちろん、資産価格が対数正規分布に従わない別のモデルを考えればこの限りではありませんが、いずれにせよ、確率論で扱うような簡潔な形で扱うのは難しく、これがドルコスト平均法の検証が困難な理由です。
まとめ
ドルコスト平均法は簡単に実施できる投資法として人気ですが、その検証は簡単ではありません。
データに依存しますし、確率論の道具を使うことができないからです。
これらを踏まえ、ドルコスト平均法の検証には、シミュレーションが有効なのではないかと考えています。
近く、シミュレーションを用いたドルコスト平均法の検証をしてみたいと思います。