
こんにちは、毛糸です。
本記事では、代数学において考察対象となる代数的構造について整理します。
群や環といった基本的な代数的構造が、それぞれどういう包含関係になっているのかを、図を用いてまとめます。
群・環・体、代数的構造の包含関係
群や環などの代数的構造は、包含関係をイメージしながら整理しておくと便利です。
たとえば
群の演算(加法)が可換であって、乗法についても閉じており、乗法の結合法則と加法乗法の分配法則が成り立つものが、環である。
というふうに、条件の緩い代数的構造(群)から始めて、条件を追加していくことでより複雑な構造(環)を得ることが出来ます。
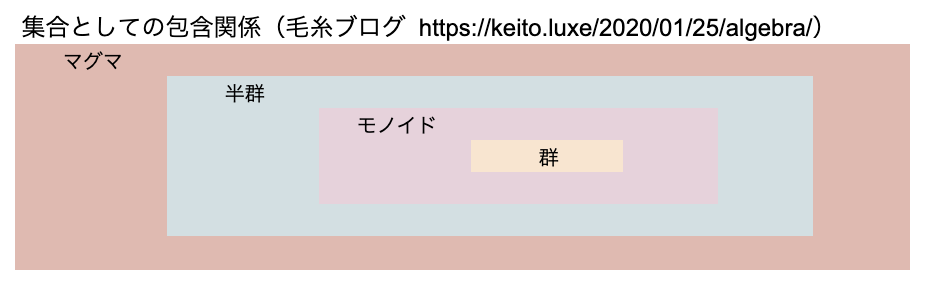
この代数的構造の包含関係を図示したものが以下です。

この図は、こちらのページ「群・環・体 (大人になってからの再学習 )」に掲載されている同様の図を参考にして、群よりも単純な代数的構造を明示し、表現を修正したものです。
なお、上の図では条件が追加されるごとに領域が大きくなっていますが、これは「集合の大きさ」を表してはいません。
条件が厳しくなれば、集合としては「狭まっていく」ので、イメージとしては以下のような感じです。
諸注意
代数的構造の包含関係図はあくまでイメージであり、正確でない表現を多分に含んでいます。
そもそも代数的構造は、ある集合と、その上の二項演算をセットで考えるものですが、上の包含関係図ではその「ある集合」とその元についての説明は省かれています。
つまり、上の包含関係図におけるマグマの説明
\(a \)と\(b \)が含まれるなら\( a+b\)も含まれる
は、
集合\( M\)の任意の元\( a\)と\( b\)について、二項演算\(+ \)が定義されていて、\( a+b\)が\( M\)の元であるとき、\( \left( M,+\right)\)をマグマと呼ぶ。
と述べるのが正確です(しかし前者の説明でも雰囲気はわかるでしょう、そのための図解です)。
また、たとえばマグマの条件を「加法について閉じている」と表現しており、二項演算を「\( +\)」で表していますが、一般にはマグマは二項演算について閉じていればよく、加法である必要はないですし(むしろ乗法と呼ぶほうが多いのかも)、二項演算を「\( +\)」で表す必然性もありません。
ただ、条件列挙の順序の観点から、群・環・体の包含関係のイメージを持つための「方便」として、あえて加法と言い「\( +\)」の記号を使っています。
その他の説明も、似たような理由から正確でない部分を含んでいますが、この図の趣旨は基本的な代数的構造の関係を直感的に捉えることですので、ご容赦ください。
正確な定義はテキストに載っていますから、そちらを参照していただくことにして、包含関係図はあくまで「直感的理解」のための使うのが良いでしょう。
代数学を理解するためのテキスト・参考書
群や環といった基本的な代数的構造を理解するためのテキストとしては、以下が入門的です。
解析学(微積分)が好きだけど、群や体の定義くらいは知っておきたい、という方は、解析学の名著「解析入門Ⅰ」の最初に、実数体を定義する際に基本的な概念が登場します。
代数学の基本的なところから始めて、最近注目を浴びている圏論も勉強したいという方は、こちらの本がまとまっています。