ベンフォード分析は財務諸表監査の一環として行われる、異常検知の手法の一つです。
本記事ではベンフォードの法則と会計監査への応用、そしてExcelでベンフォード分析を行う方法についてまとめます。
ベンフォードの法則とは「最初の桁の法則」
自然界にあるランダムかつ大量の数値データは、その最初の桁(例:123,456ならば1)に現れる数値に、ある傾向が存在する場合があります。
その傾向とは、1から9の数は均等に(一様に)現れるのではなく、1が最も多く、2、3と数字が大きくなるにつれて出現頻度が小さくなるというものです(0が桁の最初に来ることはありません)。
これをベンフォードの法則といいます。
ベンフォード分析を会計監査における異常検知に役立てようというのが、ベンフォード分析です。
監査手続としてのベンフォード分析
会計監査の対象となる仕訳データは大量です。その金額はある程度ランダムであることが予想され、ベンフォードの法則が合致するケースがあります。
仕訳データの各金額に着目して、その最初の桁が1,2,…,9となるものがそれぞれ何件あるかを調べることで、数値の分布が得られます。
その分布を見て、もしベンフォードの法則に合致しない仕訳があれば、それを異常点として認識し、より詳細な監査手続きを行うことができます。
『Excelによる不正発見法 CAATで粉飾・横領はこう見抜く』では、ベンフォード分析の結果、最初の桁が「9」の取引が大量に見つかったという事例を紹介しています。
ベンフォードの法則に従えば、「最初の桁が9」の取引データはあまり発生しないはずです。しかしこの事例では、想定よりも多い件数が見つかりました。
理由を探ろうと会社の担当者に聞いてみたところ、取引金額を「999円」と概算計上しておき、あとで正規の金額に変更するというルールがあったそうです。
もちろん、期末の決算までに金額の変更が正しく行われていれば問題ないのですが、このケースでは概算金額のまま残ってしまったのを発見したため、会社に修正を依頼したということです。
Excelによる計算
ベンフォードの法則の法則を数学的に表すと、最初の桁が\(n=1,2,\cdots,9\)である確率\( P(n)\)は
P(n)&=\log_{10}(n+1)-\log_{10}(n)\\
&=\log_{10}\left( \frac{ n+1}{ n}\right)\\
&=\log_{10}\left( 1+\frac{ 1}{ n}\right)\\
\end{split}\end{equation}
\( \log_{10}\)はExcelの関数でも簡単に計算できますから、上記の確率も簡単に計算可能です。
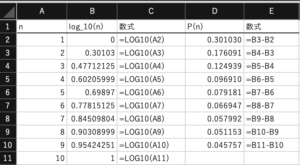
あとは分析対象となるデータの最初の桁をLEFT関数で取り出し、それをCOUNTIF関数で集計するなどして度数表をつくり、ベンフォードの法則における確率と近似しているか調べることで、Excelでベンフォード分析が行なえます。
LEFT関数の使い方については
▼Excel関数 LEFT関数を擬人化キャラクターで簡単解説 機能や使い方を簡単に説明
が参考になります。
ベンフォード分析の限界・留意点
ベンフォードの法則が成り立つとされているのは、自然界のランダムな数値データです。しかしあらゆる数値データがベンフォードの法則に従って分布しているわけではありません。
また、監査で扱うような法則性のあるデータ(従業員番号や勘定科目番号など)には適用できません。
ベンフォードの法則を利用する場合には、分析の前提や数値の分布について事前にその性質を確認しておく必要があります。
まとめ
この記事ではベンフォードの法則を利用した監査手続である、ベンフォード分析を紹介しました。
数値の分布に着目した異常検知というのは、素朴ながら一定の役立ちがあります。
Excelでも試すことができますので、是非試してみてください。
参考文献
この記事で参考にした以下の書籍は、Excelを用いた監査手続について解説を行う実務者向けの本です。昨今のデータサイエンスのように難解な数学に挑むことなく、ExcelによるComputer-Assisted Audit Techniqueを学ぶことができます。
もっとも、最近はCAATっていう言葉もあまり聞かれなくなったような気がします。コンピュータを用いた監査は、十分一般的なものになりましたからね。