こんにちは、毛糸です。
先日開発した「投資シミュレーションプログラム」は、年金運用やFXなど幅広い投資活動の分析に役立っています。
最初のバージョン以降、レバレッジと撤退の意思決定を考慮したり、ベクトル演算による高速化を行うなど、改善を続けてきました。
しかしながら、投資シミュレーションプログラムは実際の投資活動をリアルに分析するツールとしてはまだ不十分です。
今回、投資シミュレーションプログラムを更に改良し、積立投資の分析ができるようなプログラムにアップグレードしたので、その内容を解説します。
投資シミュレーションプログラムver2の改善点
今回アップデートする投資シミュレーションプログラムでは、「追加投資」の分析が行えるようになります。
従来の投資シミュレーションプログラムでは、投資期間を決めたら、期初に一括投資を行い、その後資金の出し入れは行わない前提で計算を行っていました。
しかし、実際の投資活動においては、投資資金の出し入れが行われることが通常であり、広く利用されている投資手法であるドルコスト平均法も、定期的な積立を行うものです。
今回アップデートする投資シミュレーションプログラムでは、投資期間中の資金の出入りスケジュールを計算に織り込むことができるようにします。
これにより、追加投資や引き出し、積立投資など、より現実的な分析が可能になります。
参考記事>>ドルコスト平均法の検証が難しい理由
参考記事>>ドルコスト平均法の検証が難しい理由
コード例
投資シミュレーションプログラムでは、投資スケジュールを設定することで、投資期間中の追加投資や資金の引き出しが可能になります。
具体的には、投資スケジュールを時間区分の数だけ設定し、これを期中の投資時価に反映させます。
最終的な投資時価は期中の投資スケジュールを反映させたものになり、この投資時価を何万パターンも発生させることで、将来をシミュレーションします。
資金の出入りを反映させるに伴い、まず期間を原則として月数とするようにし、投資月数をhorizonという変数に格納します。
#投資年数(自由入力) Year<-1 #1年あたりの月数(通常は12) Month_par_year<-12 #投資月数 horizon<-Year*Month_par_year#monthes
また、投資期間中の資金の出入りを、inv_schedule変数に格納します。たとえば、毎月1万円の積立投資を行う場合には、指定した数字を繰り返す関数rep()を用いて、以下のように記述します。
#投資スケジュールを入力(自由入力) inv_schedule<-rep(1,horizon)
投資のリスク・リターンも、月次ベースに直します。
#年率期待リターン(期待収益率μ、自由入力) mu<-7/100 mu_par_month<-mu/Month_par_year #年率リスク(標準偏差σ、自由入力) sigma<-12.88/100 sigma_par_month<-sigma/(Month_par_year)^0.5
シミュレーションを行う繰り返し計算の部分に、前述のinv_scheduleの各要素を足すように変更します。
#シミュレーション開始
for (s in 1:sample){
for ( t in 1:horizon){
#撤退していれば計算を飛ばす
if(W[s]==1) break
#今年の資産額=前年の資産額*(1+レバ比率*収益率)
A[s,t+1]<-A[s,t]*(1+Lev*z[s,t])+inv_schedule[t]
#もし資産額が撤退額を下回ったら撤退目印を立てる
if(A[s,t+1]<Withdraw)W[s]<-1
}
}
以上を加味した、投資シミュレーションプログラムver2.0のコードは以下のとおりです。
#投資年数(自由入力)
Year<-1
#1年あたりの月数(通常は12)
Month_par_year<-12
#投資月数
horizon<-Year*Month_par_year#monthes
#シミュレーション回数(自由入力、多いほど正確だが時間がかかる)
sample<-1000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,horizon+1)
#初期投資額を入力(自由入力)
initial<-1000
#投資スケジュールを入力(自由入力)
inv_schedule<-rep(1,horizon)
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#年率期待リターン(期待収益率μ、自由入力)
mu<-7/100
mu_par_month<-mu/Month_par_year
#年率リスク(標準偏差σ、自由入力)
sigma<-12.88/100
sigma_par_month<-sigma/(Month_par_year)^0.5
#レバレッジ比率
Lev<-1
#撤退をカウントする目印
W<-rep(0,sample)
#撤退額を設定
Withdraw<-0
#乱数を生成(ランダムな投資収益率)
set.seed(1234)
x<-rnorm(sample*horizon,mu_par_month,sigma_par_month)
#乱数(ランダムな収益率)を行列形式に変換
z<-matrix(x,sample,horizon)
#シミュレーション開始
for (s in 1:sample){
for ( t in 1:horizon){
#撤退していれば計算を飛ばす
if(W[s]==1) break
#今年の資産額=前年の資産額*(1+レバ比率*収益率)
A[s,t+1]<-A[s,t]*(1+Lev*z[s,t])+inv_schedule[t]
#もし資産額が撤退額を下回ったら撤退目印を立てる
if(A[s,t+1]<Withdraw)W[s]<-1
}
}
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の期待値は",mean(A[,horizon+1]))
#シミュレーション結果の中央値を表示
paste(Year,"年後の資産額の中央値は",median(A[,horizon+1]))
#損する確率を表示
paste("損失を被る確率は",length(A[,horizon+1][A[,horizon+1]<initial])/sample)
#億り人になれる確率を表示
paste("億り人になれる確率は",length(A[,horizon+1][A[,horizon+1]>10000])/sample)
#破産する確率を表示
paste("破産する確率は",sum(W)/sample)
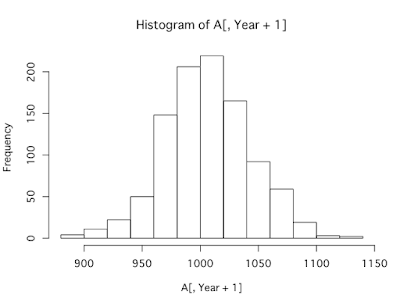
#将来の資産額の確率分布(ヒストグラム)を表示
hist(A[,Year+1])
まとめ
投資シミュレーションプログラムをアップデートし、期中の資金の出入りを考慮できるようになりました。
これにより、積立投資のシミュレーションや、資金の引き出しについての分析が行なえます。
具体的なシミュレーションの例は、近日公開予定です。
