こんにちは、毛糸です。
前回、Rライブラリ「crypto」を用いて、仮想通貨の価格が簡単に取得できることを説明しました。
>>仮想通貨の価格ヒストリカルデータを取得する方法|Rライブラリcryptoの使い方
今回は「crypto」を使って取得したBitcoin(BTC)の価格情報を分析します。
BTC価格の時系列データを分析することで、BTCの期待リターン、リスクが極めて高いことがわかりました。
また、ヒストグラムと「正規性の検定」により、BTCのリターンは正規分布に従わないこともわかりました。
目次
cryptoパッケージによるBTC価格の取得とリターンのデータ
cryptoパッケージのcrypto_history()関数を用いて、BTC価格のヒストリカルデータを取得します。
>>仮想通貨の価格ヒストリカルデータを取得する方法|Rライブラリcryptoの使い方
#crypto_history(coin = NULL, limit = NULL, start_date = NULL, #end_date = NULL, coin_list = NULL, sleep = NULL) #仮想通貨の価格等情報を取得 #dateはyyyymmdd形式で。NULLとすると最長期間 BTC<-crypto_history(coin = "BTC", start_date = NULL,end_date = NULL)
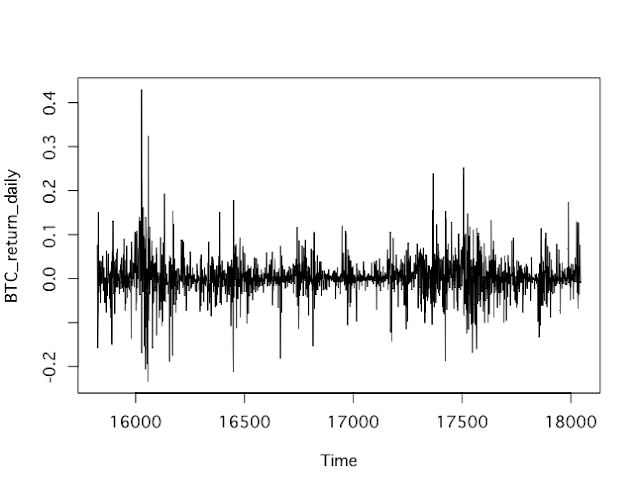
BTC_price<-ts(BTC$close,start=BTC$date[1]) plot(BTC_price,type="l")
#日次収益率 BTC_return_daily<-diff(BTC_price,lag=1)/lag(BTC_price,k=-1) plot(BTC_return_daily,type="l")
基本統計量
期待リターン(平均)
#日次収益率の平均(期待リターン)(%) mean(BTC_return_daily)*100 #[1] 0.2808807 #年率換算(%) mean(BTC_return_daily)*100*365 #[1] 102.5215
リスク(標準偏差)
#標準偏差(%) sd(BTC_return_daily)*100 #[1] 4.333606 #年率換算(%) sd(BTC_return_daily)*100*365^0.5 #[1] 82.79343
歪度
install.packages("moments")
library(moments)
分布の歪み具合を示すのが歪度です。正規分布のように左右対称な分布では、歪度は0になります。
BTC日次収益率の歪度は0.5です。歪度が正であるということは、分布のピークが左側にあり、右側の裾が広い分布であることを意味します。つまり、極端に高いリターンが出やすいと言えます。
#歪度:正規分布は0、正なら右裾が広い skewness(BTC_return_daily) #[1] 0.5234792
尖度
尖度は分布の尖り具合を示します。正規分布は尖度3(0とする定義もあり)であり、これより大きければ、分布は平均の周りで尖った、左右に裾野が広い分布になります。
BTC日次収益率の尖度は12であり、正規分布より極端に「尖った」、そして「裾野の広い」分布になります。つまり、極端に高い・低いリターンが出現しやすいことを意味します。
#尖度:正規分布が3 kurtosis(BTC_return_daily) #[1] 12.9556
BTC収益率(リターン)は正規分布にしたがうか?(正規性の検定)
ヒストグラム
リターンの実現値が、どの範囲でどのくらいの頻度で出現したかを見るグラフが、ヒストグラムです。
BTC日次収益率のヒストグラムを描いてみます。
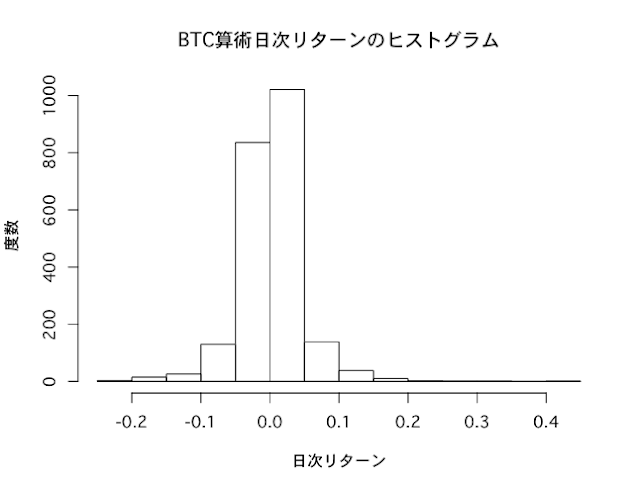
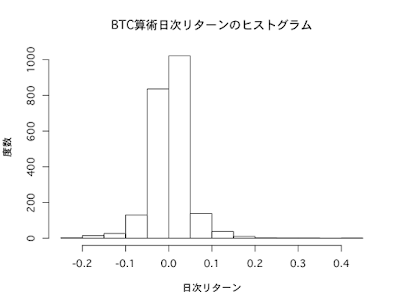
正規分布のヒストグラムは左右対称のベルのような形をしていますが、BTC収益率のヒストグラムはやや右に裾野が厚く、かつ裾野が広がっている印象を受けます。
hist(BTC_return_daily,main="BTC算術日次リターンのヒストグラム",xlab="日次リターン",ylab="度数")
Q-Qプロット
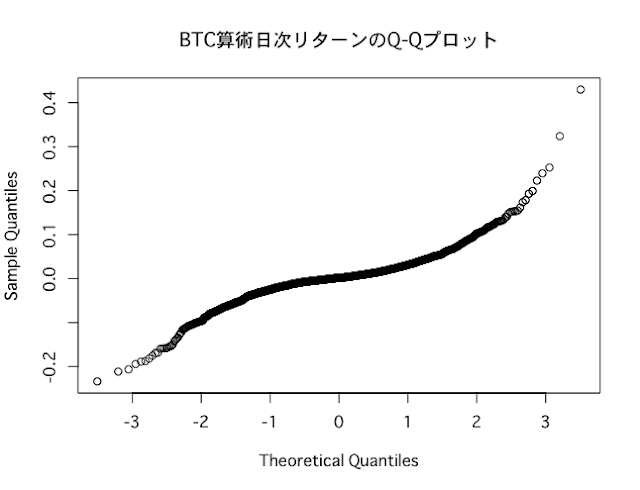
BTCの日次データをQ-Qプロットしてみると、以下のように曲線を描いており、正規分布に近いとは言えません。
qqnorm(BTC_return_daily,main="BTC算術日次リターンのQ-Qプロット")
シャピロ・ウィルク検定
> shapiro.test(BTC_return_daily) Shapiro-Wilk normality test data: BTC_return_daily W = 0.87881, p-value < 0.00000000000000022
コルモゴロフ・スミルノフ検定
> ks.test(BTC_return_daily, "pnorm", mean=mean(BTC_return_daily), sd=sqrt(var(BTC_return_daily))) One-sample Kolmogorov-Smirnov test data: BTC_return_daily D = 0.11752, p-value < 0.00000000000000022 alternative hypothesis: two-sided 警告メッセージ: ks.test(BTC_return_daily, "pnorm", mean = mean(BTC_return_daily), で: コルモゴロフ・スミノフ検定において、タイは現れるべきではありません
ビットコインの収益率が正規分布に従わないとなにが困るか
このように、確率分布が標準的なファイナンスの仮定と異なることにより、やや慎重な議論が必要になってきます。
投資においては、為替や株式等よりも変動性が大きく、また極端に高いもしくは低いリターンが出やすいという点に気をつける必要があります。
まとめ
ビットコインを始めとする仮想通貨のデータを扱う際には、この分布の特性をよく踏まえる必要があります。
関連記事>>ビットコインはバブルである
参考記事