こんにちは、毛糸です。
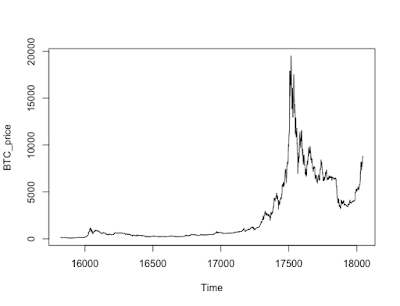
2019年6月26日現在、ビットコイン価格が再び高騰しており、135万円を超えました。
ビットコインを始めとする仮想通貨(暗号資産)は2017年頃に劇的な価格高騰を引き起こし、現代の「バブル」として社会に大きな影響を与えました。
参考記事>>ビットコインはバブルである
リンクの記事でも述べたとおり、仮想通貨はキャッシュフローの裏付けがなく、厳密な意味で「資産」と呼べるか微妙な投資対象です。
基本的には「明日は今日より高くなる」という期待が価格形成に寄与する「バブル」的性格を持つと考えれます。
バブル資産としての仮想通貨は、その特徴的な価格変動やリターンの非正規性など、既存のファイナンス理論では説明しづらい部分が多くあります。
>>ビットコインの確率分布について|期待リターン、リスク、ヒストグラム【正規分布じゃない】
仮想通貨を理論的に扱おうとする場合には、バブル資産としての特徴を考慮する必要がありますが、バブル資産の理論研究は相対的に未成熟な分野です。
本記事ではファイナンス(金融工学)の立場からバブル資産を研究した文献をメモしておきます。
目次
Continuous-Time Asset Pricing Theory: A Martingale-Based Approach(by R. Jarrow)
Robert Jarrowによるテキスト “Continuous-Time Asset Pricing Theory: A Martingale-Based Approach“には、バブル資産に関する比較的新しい研究成果が簡潔にまとまっています。
Jarrowは金利モデルで有名なヒース・ジャロー・モートンモデルの開発者のひとりです。
本書では、バブル資産を「局所マルチンゲール」という確率過程としてモデル化しており、おそらくこのアプローチが現在のバブル資産の標準的モデルと考えられます。
Jarrowはバブル資産に関する数多くの論文を執筆しており、本書はその研究成果のまとめとしても活用できるため、バブル資産の理解を深めたいと思ったら手に取るとよいでしょう。
リンク
A Mathematical Theory of Financial Bubbles(by P. Protter)
P. Protterによるノート”A Mathematical Theory of Financial Bubbles“は、前述のJarrowのテキストにも引用される、バブル資産の先駆的研究です。
こちらもバブル資産を「局所マルチンゲール」としてモデル化し種々の分析を行っています。
局所マルチンゲールを含む確率過程論や確率微分方程式という数学は、理系大学の学部後半から大学院にかけて学ぶ内容であり、比較的高度です。
ファイナンスの数理的研究はこうした確率論と密接に結びついていますので、バブルの研究にも確率論の勉強は避けては通れないでしょう。
ファイナンスにも言及している、確率過程や確率微分方程式を扱ったテキストとしては以下が参考になります。
リンク
局所マルチンゲールとバブル(村上祐亮 著)
バブルに関する日本語の文献では、九州大学院の修士論文「局所マルチンゲールとバブル」(村上祐亮)が参考になります(PDFリンク)。
この論文ではファイナンスに関する確率論の基本事項を完結にまとめながら、バブル資産を局所マルチンゲールとしてモデル化し、種々の性質や具体例について説明しています。
JarrowのテキストやProtterのノートは英語ですが、こちらは日本語で書かれているので、数学の壁さえクリアできれば読みやすいかも知れません。
余談ですが、九州大谷口教授は確率論研究で有名な先生で、彼のゼミの修士論文は大変勉強になるので、よく参考にしています(谷口ゼミ修士論文一覧リンク)。
まとめ
本記事ではバブル資産に関する最近の研究を知るための文献をまとめました。
バブル資産に関する研究は比較的新しく、勉強しがいのある分野です。
本記事で取り上げた文献を丁寧に読み解けば、仮想通貨投資に役立てられる可能性もありますので、野心的な方は挑戦してみてください。