こんにちは、毛糸です。
株式の期待リターンを推定するために広く用いられているのが、CAPM(Capital Asset Pricing Model)です。
CAPMは株式のリターンを市場ポートフォリオの1次関数として表す、とてもわかり易いモデルです。
本記事ではCAPMの計算(具体的には、ベータの推定)を、統計プログラミング言語Rで行う方法についてまとめます。
CAPMにおけるベータの推定には、個別株式と市場ポートフォリオのリターンのデータが必要になりますが、quantmodというパッケージを使えば、簡単に取得できるため、その方法も説明します。
また、推定に必要な無リスク金利(安全資産利子率)には、財務省が公表している国債利回りを用いることとします。
CAPM(Capital Asset Pricing Model、資本資産価格モデル)の概略
CAPMは、資産収益が正規分布するなどのいくつかの仮定のもとで成り立つ、危険資産(株式など)の期待リターンに関するモデルです。
CAPMでは、ある証券\( i\)の期待リターン\( E[r_i]\)は、無リスク金利\( r_f\)と市場ポートフォリオの期待リターン\( E[r_M]\)を用いて、以下のように表されます。
\begin{equation} \begin{split}
E[r_i]=r_f+\beta\left( E[r_M]-r_f\right)
\end{split} \end{equation}
係数の\( \beta\)(ベータ)は、証券\( i\)と市場ポートフォリオ\( M\)の連動性を示しています。
CAPMにおける\( \beta\)は、ある証券\( i\)の超過期待リターン\( E[r_i]-r_f\)を被説明変数、市場ポートフォリオの超過期待リターン\( E[r_M]-r_f\)を説明変数とした回帰分析によって求められます。
本記事では、統計プログラミング言語Rを用いて、
- 証券と市場ポートフォリオのデータを取得しリターンを計算する方法
- 無理リスク金利を取得する方法
- 回帰分析を行う方法
を解説しています。
quantmodによる株価ヒストリカルデータの取得方法
Rライブラリ「quantmod」を用いると、個別株式の価格情報を入手することができます。
quantmodは、Rコンソールで以下を実行すればインストールできます。同時に「XML」というライブラリも必要になる(ないとエラーを吐く)ので、合わせてインストールしましょう。
install.packages(“quantmod”)
install.packages(“XML”)
quantmodライブラリを読み込みます。
library(quantmod)
getSymbols()関数を使うと、指定した証券コードの価格データをwebページから取得することができます。日本の株式では、Yahoo!ファイナンスを情報ソースにすればよいです。
本記事では、証券コード9984.Tソフトバンクグループの株価を、Yahoo!ファイナンスから、開始日”2013-06-01″、終了日”2019-05-31″で取得します。
証券コードは、Yahoo!ファイナンスの各証券のページの?code=以下に記載されているものです。
https://stocks.finance.yahoo.co.jp/stocks/detail/?code=9984.T
証券コードの.Tは市場(T=東京証券取引所)を示すものですが、なくても大丈夫かもしれません。
関数の最後の引数auto.assignは取得したデータを自動でオブジェクトに代入するかどうかを決めるもので、=TRUEとした場合は自動的に「YJ9984.T」というオブジェクトに情報が格納されます。
getSymbols(“9984.t”,src=”yahooj”,from=”2013-06-01″,to=”2019-05-31″,auto.assign=TRUE)
auto.assign=FALSEとした場合には自動でオブジェクトに代入されないので、自分でオブジェクトに代入します。
data9984<-getSymbols(“9984.t”,src=”yahooj”,from=”2013-06-01″,to=”2019-05-31″,auto.assign=FALSE)
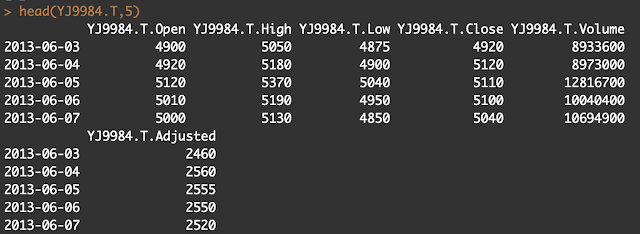
取得したデータは、日次ベースの時系列データになっており、始値・高値・安値・終値・取引高・調整後株価が格納されています。
以下の作業では終値の情報を使いますので、以下のように終値のみのデータを作ります。
Price_i<-YJ9984.T$YJ9984.T.Close
plotすることで株価の推移を見ることができます。
plot(Price_i)
\( t\)日目の日次リターン\( r_{i,t}\)は
\begin{equation} \begin{split}
r_{i,t}=\frac{P_{i,t} -P_{i,t-1}}{ P_{i,t-1}}\approx \log(P_{i,t})-\log(P_{i,t-1})
\end{split} \end{equation}
r_{i,t}=\frac{P_{i,t} -P_{i,t-1}}{ P_{i,t-1}}\approx \log(P_{i,t})-\log(P_{i,t-1})
\end{split} \end{equation}