このブログでは【君の知らない複式簿記】と題して、複式簿記の一風変わった側面を紹介しています。
そのなかで、複式簿記を代数学の言葉で表現しようという試みを行っています。この分野を簿記代数と呼んでいます。
簿記代数があるなら、簿記幾何があってもいいのでは!?
ということで、この記事では簿記幾何の展望についてお話します。
複式簿記は有向グラフで表せる
複式簿記における仕訳や試算表は、向きを持った矢印の集合体で表せます。これを有向グラフといいます。
たとえば、
\mbox{(借)}&\mbox{固定資産}&1000&/\mbox{(貸)}&\mbox{現金}&1000\\
\end{array}\]
という仕訳は、貸方の「現金」勘定から借方の「固定資産」勘定に向かう矢印として、次のような有向グラフとして表現できます。
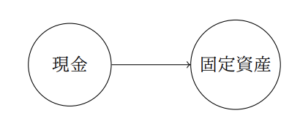
もっと複雑な仕訳も有向グラフにできます、以下はどんな仕訳かわかりますか?
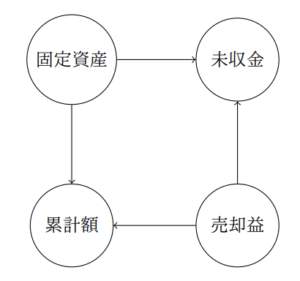
グラフ理論とトポロジー(位相幾何学)
複式簿記を有向グラフで表現できれば、グラフに関する理論が使えるのではないかと期待できます。グラフ理論やトポロジー(位相幾何学)と呼ばれる分野がそれに該当します。
グラフ理論は線形代数と関係があります。複式簿記の有向グラフを線形代数の手法によって分析し、財務諸表から期中の取引を推定する研究がすでにあります(参考文献を参照してください)。
トポロジー、特に代数的位相幾何学と呼ばれる分野では、幾何学の問題に代数の考え方を用いるような研究領域です。トポロジーでは多面体を一般化した「複体」というものが重要な役割を果たします。
簿記幾何、簿記トポロジー(簿記トポ)に向けて
複式簿記の有向グラフを複体として表せないか、というアイデアは、簿記の有向グラフ表現を見た人であれば興味を持っていただけるでしょう。ただ、今のところ、私の理解はあまり進んでいません。
トポロジーでは高次元の複体(≒多面体)の境界をとるという操作が繰り返し行えるようなものを考えます。これをチェイン複体といいます。
複式簿記がチェイン複体として考察できればとても面白いのですが、素朴なやり方ではあまりうまく行きません。複式簿記の有向グラフは勘定を頂点、仕訳を辺(矢印)に見立てて作りますので、何度も繰り返し境界をとるという操作を考えるのが難しいのです。
そこで別の方法を考えます。それは、仕訳や試算表の取りうる範囲を複体として表せないか、というアイデアです。これなら点も辺も面も扱えます。
一般にn個の勘定を持つ会計システムにおいて、仕訳や試算表はn次元空間の点として表せるので、仕訳や試算表の取りうる範囲もn次元空間の一部です。このような仕訳の範囲は形を持っているので、それを複体として扱えないだろうかということです。
n次元空間の一部として「簿記複体」を考えると、その境界を取るという操作も繰り返し行えそうな気がします。多面体から面へ、面から辺へ、辺から点へという境界をとる操作が都合よく展開できれば、複式簿記を幾何学的に捉えることが可能になり「仕訳の形」が見えてくるのではないかと考えています。
まとめと参考文献
複式簿記を幾何学的に考えることについてお話しました。簿記幾何、簿記トポロジー、簿記トポの研究は始まったばかりです。
ちなみに、なんの役に立つのかはわかりません。でも、複式簿記というビジネスの基本言語が数学の一大分野と関連していることがわかれば、きっと複式簿記の知らない性質が見えてくるはずです。
当面はトポロジーに関する勉強を進めたいと思います、以下のテキストがわかりやすくAmazonの評価も高いです。
複式簿記や会計のトピックを、線形代数やグラフ理論などの数理科学的手法によって考察する研究を行っている研究者もいらっしゃいます。たとえば、雑誌『企業会計』2021年1月号からの連載『会計,数理科学と出会う』では、そうした研究を垣間見ることができます。
私が簿記トポロジーへの挑戦を決めたのは、『数学ガール』でトポロジーに関するトピックを扱っていたことも関係しています。シリーズが豊富ですが、以下で紹介する「ポアンカレ予想」では、トポロジーや抽象代数について理解を深められます。ストーリーも秀逸で、心動かされること必至です。
トポロジーの教材について、ネットでアクセス可能なものにも、大変ありがたい資料がいくつもあります。
やわらかい穴から形をみてみよう 平岡裕章(九州大学)(PDFが開きます)
幾何学 C ホモロジー論入門 福井 敏純(PDFが開きます)
トポロジーへの招待 〜 3. ホモロジー群の構成とオイラー数の正体
複式簿記を代数の言葉で表現する簿記代数については下記をご覧ください。
コメント