目次
- 1 【君の知らない複式簿記】とは
- 2 【君の知らない複式簿記0】まだ見たことのない複式簿記の姿を追い求めて
- 3 【君の知らない複式簿記1】行列簿記の意義、性質、限界
- 4 【君の知らない複式簿記2】複式簿記の拡張、三式簿記
- 5 【君の知らない複式簿記3】複式簿記の代数的構造「群」
- 6 【君の知らない複式簿記4】簿記代数の教科書『Algebraic Models For Accounting Systems』とバランスベクトル
- 7 【君の知らない複式簿記5】簿記とベクトル、行列、そしてテンソルへ
- 8 【君の知らない複式簿記6】矢印簿記で仕訳をビジュアライズ
- 9 【君の知らない複式簿記7】T勘定とパチョーリ群
- 10 【君の知らない複式簿記8】会計は写像であり、関手である。
- 11 【君の知らない複式簿記 補遺】BSの微分はPLである、とはどういうことか
- 12 【君の知らない複式簿記 補遺】誘導法によるキャッシュ・フロー計算書とバランス・ベクトル
- 13 【君の知らない複式簿記 補遺】隣接行列とマテシッチの行列簿記
- 14 【君の知らない複式簿記 補遺】複式簿記の座標
- 15 【君の知らない複式簿記 補遺】ブロックチェーン的三式簿記の3つの解釈
- 16 【君の知らない複式簿記 補遺】シェアーによる借方・貸方の説明と矢印簿記
- 17 参考文献
【君の知らない複式簿記】とは
【君の知らない複式簿記】は毛糸ブログのシリーズ記事のひとつです。
資格試験や学校教育では通常習わないような、複式簿記の普段とは違う側面に焦点を当てた解説を行っています。
以下のようなキーワードを含んでいます。
- 三式簿記(時制的三式簿記、微分的三式簿記、ブロックチェーン的三式簿記)
- 行列簿記
- 簿記代数(複式簿記の代数構造)
【君の知らない複式簿記0】まだ見たことのない複式簿記の姿を追い求めて
こちらの記事では、【君の知らない複式簿記】シリーズを書こうと思ったきっかけについて述べています。
複式簿記は複雑極まりない企業の状態や取引を、複式簿記の枠組みから外れることなく描ききる、「美しい」機構です。
その美しさの源はどこにあるのか、複式簿記を理解した先に何を求めるのか、私の思いを書いています。
【君の知らない複式簿記1】行列簿記の意義、性質、限界
こちらの記事では、複式簿記を「行列」で表現する方法について解説しています。
複式簿記の借方貸方という独自概念を、行と列に対応して表現する方法です。
行列簿記は、取引の詳細を把握したり、原価計算における配賦問題に応用したりといった活用方法があります。
【君の知らない複式簿記2】複式簿記の拡張、三式簿記
こちらの記事では、複式簿記の拡張について解説しています。
「複式簿記は完全なものか?」という深遠な問いかけをした会計学者がいました。名前は井尻雄士先生。
彼は複式(二式)簿記を三式簿記に拡張することで、簿記を拡張させました。
記事では、昨今話題のブロックチェーンによる三式簿記についても触れています。
財産=資本
ストック=フロー
【君の知らない複式簿記3】複式簿記の代数的構造「群」
こちらの記事では、試算表や仕訳などの複式簿記におけるオブジェクトの集合が、群であることを解説しています。
群の公理を示し、試算表に仕訳を追加して新たな試算表を得るという手続き(演算)を考えることで、試算表の集合が群であることを解説しています。
- 仕訳の追加について閉じている
- 仕訳順序によらない(結合法則)
- 仕訳なしの存在(単位元)
- 逆仕訳の存在(逆元)
【君の知らない複式簿記4】簿記代数の教科書『Algebraic Models For Accounting Systems』とバランスベクトル
こちらの記事では、簿記代数のテキストについて紹介しています。
テキストで紹介される、バランスベクトルによる会計システムの表現は、簿記代数の基礎となります。
バランスベクトルの定義と群としての性質について簡潔にまとめています。
【君の知らない複式簿記5】簿記とベクトル、行列、そしてテンソルへ
こちらの記事では、複式簿記のバランスベクトル表現を、行列とテンソルに拡張するアイデアについて解説しています。
バランスベクトルの要素は勘定科目に対応していましたが、勘定科目とは別の「軸」を取り入れることで、バランス行列やバランステンソルという概念を定義します。
バランステンソルは会計システムの情報量を増やし、より多様な会計情報を表現するのに役立ちます。
T^D=\left(a_{ i_1,\cdots,i_D }\right)
\end{split} \end{equation}
\sum_{i_1} a_{ i_1,\cdots,i_D }=\cdots=\sum_{i_D} a_{ i_1,\cdots,i_D }=0
\end{split} \end{equation}
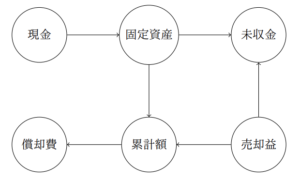
【君の知らない複式簿記6】矢印簿記で仕訳をビジュアライズ
こちらの記事では、有向グラフという図によって複式簿記を「描く」方法について、その理論的背景とともに解説しています。
仕訳がバランスベクトルとして表現できることを用いて、これを矢印で表現することで、会計システムの構造や性質を知ることが可能になり、会計と簿記の理解が深まることが期待されます。
【君の知らない複式簿記7】T勘定とパチョーリ群
こちらの記事では、複式簿記におけるT勘定図(Tフォーム)を順序対として表現した時に得られる群構造、パチョーリ群について解説しています。
パチョーリ群は勘定の借方合計・貸方合計を順序対で表現し、貸借差額が一致するようなTフォームを同一視することで得られる群です。1980年代から研究されており、最近も関連する論文が公表されています。
\mathcal{P}&=\mathcal{A}/\simeq\\
&=\left\{ C([d//c])|d,c\in \mathbb{R},d,c\geq 0\right\}
\end{split} \end{equation}
【君の知らない複式簿記8】会計は写像であり、関手である。
こちらの記事では、「会計は写像である」という有名なフレーズを数学的に定式化してえられる「会計写像」が、経済状態の圏\( \mathscr{ S }\)と会計情報の圏\( \mathscr{ A }\)をつなぐ関手となることを示しています。
いわば会計は、経済状態と会計情報の架け橋、もしくは経済状態の情報的なアナロジーになっています。
\alpha_A:\mathscr{ S }\to \mathscr{ A }
\end{split} \end{equation}
【君の知らない複式簿記 補遺】BSの微分はPLである、とはどういうことか
こちらの記事では、「BSの微分はPL」という主張について、いくつかの仮定と数学的な証明、そしてよくある誤解についてまとめています。
\Delta \mathrm{BS}=\mathrm{PL}(t+\Delta t)
\end{split} \end{equation}
【君の知らない複式簿記 補遺】誘導法によるキャッシュ・フロー計算書とバランス・ベクトル
こちらの記事では、キャッシュ・フロー計算書を損益計算書と同じように作成する方法(誘導法)について解説します。
誘導法によるキャッシュ・フロー計算書とは、期中の仕訳においてキャッシュ・フロー科目を明示的に登場させ、貸借対照表のキャッシュの科目を用いない方法です。
【君の知らない複式簿記 補遺】隣接行列とマテシッチの行列簿記
こちらの記事では、グラフ理論に登場する隣接行列について解説しています。
【君の知らない複式簿記1】で紹介した(マテシッチの)行列簿記は、この隣接行列の具体例になっています。
【君の知らない複式簿記 補遺】複式簿記の座標
こちらの記事では、以下の記事で解説した「複式簿記のベクトル表現」であるバランスベクトルに関連して、勘定科目が座標を決めるということについて解説しています。
【君の知らない複式簿記4】簿記代数の教科書『Algebraic Models For Accounting Systems』とバランスベクトル
【君の知らない複式簿記 補遺】ブロックチェーン的三式簿記の3つの解釈
こちらの記事では、以下の記事で触れたブロックチェーン的三式簿記において、文献によって3つの異なる意味付けがなされていることを整理しています。
【君の知らない複式簿記 補遺】シェアーによる借方・貸方の説明と矢印簿記
こちらの記事では、100年前の会計学者シェアーが述べた「貸方は始点、借方は終点」という主張について、矢印簿記との繋がりを指摘しています。
参考文献
【君の知らない複式簿記】シリーズでは、数学的な考え方を多用します。したがって、通常の簿記論の訓練だけでは、十分な理解が得られない可能性があります。
各記事には参考文献が載っています。その他にも、以下の記事にテキスト・参考書がまとめてあります。
コメント