会計士や経理人材は、仕事の中でたくさんの「表(テーブル)」を目にします。表の各列の合計額(縦計)と各行の合計額(横計)をそれぞれ集計することで、表の概要がわかります。
ここで重要なことは、縦計の合計額(つまり、縦計の横計)と、横計の合計額(つまり、横計の縦計)は一致するということです。
私たちはこの性質に依拠して、集計ミスを発見します。縦計合計と横計合計が一致しない場合、各縦計もしくは横計のいずれかに集計ミスがあることを意味するため、チェック機能を果たすのです。
しかし、そもそもなぜ縦計の合計と横計の合計は一致するのでしょうか?
この素朴な問いかけに対して、数学的な回答を考えてみます。
目次
表(テーブル)を行列として表す
この記事では、表(テーブル)を行列として表します。すなわち、この記事において表とは、いくつかの実数を長方形に規則正しく並べたものとして定義します。
このような定義に当てはまるものであれば、表の「意味」は問いません。あくまで行列として表せる実数の集合体を表と定義します。
表を以下のような\( n\times m\)行列\( A\)として表します。
A
= \left(
\begin{array}{rrr}
a_{1,1} & a_{1,2} & \cdots &a_{1,m}\\
a_{2,1} & a_{2,2} & \cdots &a_{2,m}\\
\vdots & \vdots & \ddots & \cdots\\
a_{n,1} & a_{n,2} & \cdots &a_{n,m}
\end{array}
\right)
\end{split}\end{equation}
この表は、縦に\( n\)個、横に\( m\)個の数字を並べてできる表を示しています。各\( a_{i,j}(1\leq i\leq n,1\leq j\leq m)\)には適当な実数が入ります。\( n,m\)は1以上の整数であれば何でも構いません。
例
以下の図は三菱UFJフィナンシャル・グループの2020年3月期の有価証券報告書から抜粋したものです。
保有する資産を縦方向に、時価の「複雑度」としてのレベルを横方向に配置し、表内の各数字は2020年3月末時点の保有残高を意味しています。
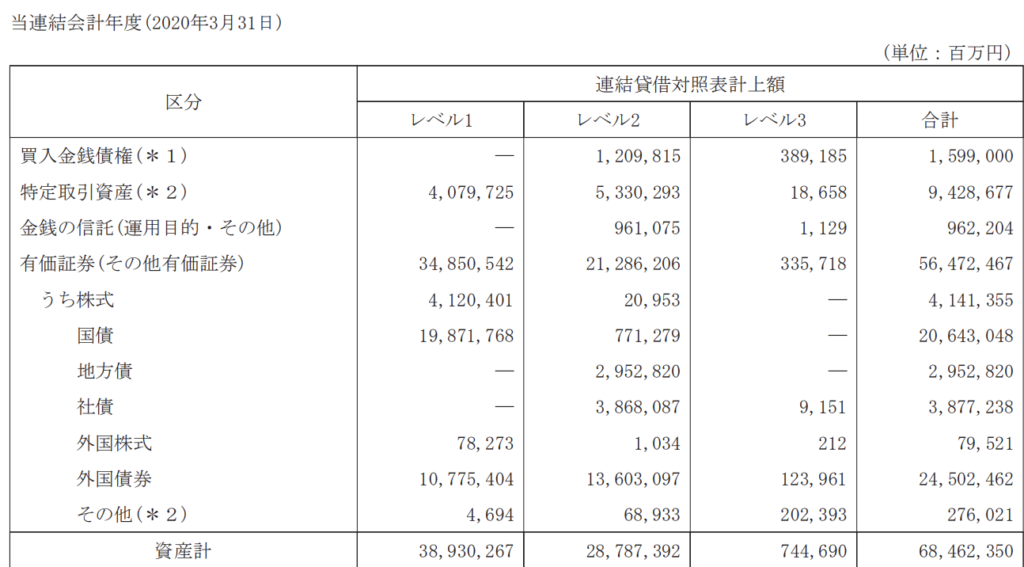
この表には、縦計として「資産計」欄が、横計として「合計」欄が設けられています。それぞれの合計は68,462,350(百万円)で一致しています(ただし百万円未満の端数調整が行われているため、厳密にピッタリ一致はしません。)
この表を行列として表すと、次のようになります(「有価証券(その他有価証券)」の内訳を無視します)。
\left(
\begin{array}{rrr}
0& 1,209,815 &389,185\\
4,079,725 &5,330,293 &18,658\\
0& 961,075& 1,129\\
34,850,542 &21,286,206 &335,718
\end{array}
\right)
\end{split}\end{equation}
縦計をシグマ記号で表す
ある表を
A
= \left(
\begin{array}{rrr}
a_{1,1} & a_{1,2} & \cdots &a_{1,m}\\
a_{2,1} & a_{2,2} & \cdots &a_{2,m}\\
\vdots & \vdots & \ddots & \cdots\\
a_{n,1} & a_{n,2} & \cdots &a_{n,m}
\end{array}
\right)
\end{split}\end{equation}
\begin{array}{c}
a_{1,1}\\
+\\
a_{2,1}\\
+\\
\vdots\\
+\\
a_{n,1}\end{array}
\end{split}\end{equation}
\sum_{i=1}^n a_{i,1}=a_{1,1}+a_{2,1}+\cdots+a_{n,1}
\end{split} \end{equation}
列番号を具体的に指定せず、変数\( j\)を用いて、この表\( A\)の第\( j\)列の縦計を考えると
\sum_{i=1}^n a_{i,j}=a_{1,j}+a_{2,j}+\cdots+a_{n,j}
\end{split} \end{equation}
もともとの表\( A\)の最終行に「縦計」を追加すると、以下のように表すことができます。
\left(\begin{array}{c} A \\ \hline \mbox{縦計}\end{array}
\right)
= \left(
\begin{array}{ccc}
a_{1,1} & a_{1,2} & \cdots &a_{1,m}\\
a_{2,1} & a_{2,2} & \cdots &a_{2,m}\\
\vdots & \vdots & \ddots & \cdots\\
a_{n,1} & a_{n,2} & \cdots &a_{n,m}\\
\hline
\sum_{i=1}^n a_{i,1} &\sum_{i=1}^n a_{i,2} &\cdots &\sum_{i=1}^n a_{i,m}
\end{array}
\right)
\end{split}\end{equation}
縦計の合計(縦計の横計)
各列の縦計を横に並べて書くと、
\mbox{縦計}= \left(\sum_{i=1}^n a_{i,1}, \sum_{i=1}^n a_{i,2}, \cdots, \sum_{i=1}^n a_{i,m}
\right)
\end{split}\end{equation}
この横ベクトルの各要素をすべて足し合わせたものは縦計の合計であり、縦計の横計とも表現できます。これを和の記号\( \sum\)をもう一つ使って表すと
\sum_{i=1}^n a_{i,1}+ \sum_{i=1}^n a_{i,2}+ \cdots, \sum_{i=1}^n a_{i,m}=\sum_{j=1}^m \sum_{i=1}^n a_{i,j}
\end{split} \end{equation}
結論をもう一度書くと、縦計の合計は
\sum_{j=1}^m \sum_{i=1}^n a_{i,j}
\end{split} \end{equation}
横計をシグマ記号で表す
A
= \left(
\begin{array}{rrr}
a_{1,1} & a_{1,2} & \cdots &a_{1,m}\\
a_{2,1} & a_{2,2} & \cdots &a_{2,m}\\
\vdots & \vdots & \ddots & \cdots\\
a_{n,1} & a_{n,2} & \cdots &a_{n,m}
\end{array}
\right)
\end{split}\end{equation}
a_{1,1}+a_{1,2}+\cdots+a_{1,m}
\end{split} \end{equation}
\sum_{j=1}^m a_{1,j}=a_{1,1}+a_{1,2}+\cdots+a_{1,m}
\end{split} \end{equation}
列番号を具体的に指定せず、変数\( i\)を用いて、この表\( A\)の第\(i\)行の横計を考えると
\sum_{j=1}^m a_{i,j}=a_{i,1}+a_{i,2}+\cdots+a_{i,m}
\end{split} \end{equation}
もともとの表\( A\)の最終列に「横計」を追加すると、以下のように表すことができます。
\left(A |\mbox{横計}\right)
= \left(
\begin{array}{cccc|c}
a_{1,1} & a_{1,2} & \cdots &a_{1,m}&\sum_{j=1}^m a_{1,j}\\
a_{2,1} & a_{2,2} & \cdots &a_{2,m}&\sum_{j=1}^m a_{2,j}\\
\vdots & \vdots & \ddots & \cdots&\vdots\\
a_{n,1} & a_{n,2} & \cdots &a_{n,m}&\sum_{j=1}^m a_{n,j}
\end{array}
\right)
\end{split}\end{equation}
横計の合計(横計の縦計)
各列の横計を縦に並べて書くと、
\mbox{横計}=
\left(
\begin{array}{c}
\sum_{j=1}^m a_{1,j}\\
\sum_{j=1}^m a_{2,j}\\
\vdots\\
\sum_{j=1}^m a_{n,j}
\end{array}
\right)
\end{split}\end{equation}
この縦ベクトルの各要素をすべて足し合わせたものは横計の合計であり、横計の縦計とも表現できます。これを和の記号\( \sum\)をもう一つ使って表すと
\sum_{j=1}^m a_{1,j}+ \sum_{j=1}^m a_{2,j}+ \cdots \sum_{j=1}^m a_{n,j}=\sum_{i=1}^n \sum_{j=1}^m a_{i,j}
\end{split} \end{equation}
結論をもう一度書くと、 横計の合計は
\sum_{i=1}^n \sum_{j=1}^m a_{i,j}
\end{split} \end{equation}
縦計と横計の合計一致定理
縦計の合計は
\sum_{j=1}^m \sum_{i=1}^n a_{i,j}
\end{split} \end{equation}
\sum_{i=1}^n \sum_{j=1}^m a_{i,j}
\end{split} \end{equation}
ここで和に関する重要な性質を思い出します。それは、有限個の実数の和は、足し算の順番と関係ないということです。
実数\(a,b\)に対して、\( a+b\)と\( b+a\)は一致します。この規則は交換法則とよばれます。
足し合わせる実数が2つより大きくても(有限個であれば)交換法則が成り立ちます。たとえば\( a_1+a_2+\cdots+a_n=a_n+\cdots+a_2+a_1\)のように表すことができ、足し算の順番は関係ありません。
さらに、添え字が複数(今回であれば\( i\)と\( j\))であっても、足し合わせる個数(今回であれば\(n\)個と\( m\)個)が有限であれば、足し算の順番を入れ替えることが許されます。したがって、変数\( i\)について和をとってから変数\( j\)について和をとった場合と、変数\( j\)について和をとってから変数\( i\)について和をとった場合とは一致します。つまり\( \sum_{i=1}^n\)と\( \sum_{j=1}^m\)の順番は入れ替えても良いということです(See.トネリの定理)。
以上のことから、私たちは
\sum_{j=1}^m \sum_{i=1}^n a_{i,j}=\sum_{i=1}^n \sum_{j=1}^m a_{i,j}
\end{split} \end{equation}
私たちは表(テーブル)を行列として表現することで、縦計の合計と横計の合計は一致するという命題「縦計と横計の合計一致定理」を証明できました。
なお、\( \sum_{j=1}^m \sum_{i=1}^n a_{i,j}=\sum_{i=1}^n \sum_{j=1}^m a_{i,j}\)からわかることとして、「縦計・横計のそれぞれの合計は、表に登場する\( a_{i,j}\)をすべて足したものである」という性質もわかります。
発展的な内容
無限個の和
縦計と横計の合計一致定理は、有限個の和は順番によらないという性質によって成り立つ定理といえます。
しかし、和が無限個になると順番を気にしなくてはならなくなります。例えば\( S=1-1+1-1+\cdots\)という無限個の和は、その順番次第で
S=(1-1)+(1-1)+\cdots=0\\
S=1+(-1+1-1-1+\cdots)=1
\end{split} \end{equation}
フビニの定理
和の記号\( \sum\)は、\( 1,2,3,\cdots\)と数えられるような数の和を簡略的に表すことができるのでした。
和に関する記号としては他に、積分記号のインテグラル\( \int\)があります。
縦計と横計の合計一致定理の証明のなかで\( \sum_{i=1}^n \sum_{j=1}^m\)の順序を入れ替えたように、重なった積分記号\( \int_{a}^{b}\int_{c}^{d}\)を入れ替えることも可能です(もちろん条件が必要です)。
このような積分の交換は、フビニの定理とよばれます。
まとめと参考文献
この記事では表(テーブル)を実数行列として表し、縦計と横計のそれぞれの合計額が一致することを証明しました。
縦計・横計の一致は数字を扱う業務ではしばしば用いられる性質ですが、それは数学的に確かな性質なのだということがおわかりいただけたと思います。
行列は最近の高校課程では習わないようですが、その基本的な計算方法くらいは知っておいて損はありません。
以下のテキストは行列を含む高校数学の復習に適した書籍です。