こんにちは、毛糸です。
私は投資信託に積立投資を行っており、そのなかでアクティブファンドである「ひふみ投信」を購入しています。
参考記事:【投信定点観測】インデックス投資信託8つ・ロボアドバイザー2つ・アクティブファンド3つにドルコスト平均法で積立投資してみる
ひふみ投信は主に日本株式を中心に運用を行うアクティブファンドで、中小型株の目利き力に優れた投資信託として個人的に注目しています。
そんなひふみ投信ですが、最近ネットではパフォーマンスに疑問符を投げかける声が散見されています。
そこで今回は、ひふみ投信に対するネガティブな声に反論すべく、ひふみ投信の優位性を統計学的に検証してみたいと思います。
結論として、ひふみ投信は日本株式のインデックスであるTOPIXに対する勝率が、有意に1/2を超える結果となりました。
目次
価格時系列データはYahoo!ファイナンスから
ひふみ投信とTOPIXのデータはYahoo!ファイナンスから取得しました。
9C31108Aひふみ投信の時系列データはこちら。
TOPIXの時系列データはこちら。
ひふみ投信は基準価格を、TOPIXは終値をそれぞれ使用します。
期間はひふみ投信の設定開始日2008/10/1から本記事執筆時点の直近営業日である2019/4/26までの、2,590日です。
日次リターン(算術、純額表示)の計算
日次の算術リターン(日次リターン、純額表示)を計算します。
\( t\)日目のリターン\( r_t\)は、\( t\)日目の価格\( S_t\)と\( t-1\)日目の価格\( S_{t-1}\)を用いて、以下の計算式で算出します。
r_t=\frac{ S_t-S_{t-1}}{ S_{t-1}}=\frac{S_t }{S_{t-1} }-1,~r_1=1
\end{split} \]
この計算により、ひふみ投信の日次リターン\( r_t^H\)とTOPIXの日次リターン\( r_t^T\)(\( t=1,2,\cdots,2590\))が得られます。
ひふみ投信とTOPIXの日次リターンの平均
ひふみ投信とTOPIXの日次リターンの分散、標準偏差(リスク)
ひふみ投信とTOPIXの日次リターンのシャープ・レシオ
ひふみ投信とTOPIXの日次リターンの累積リターン
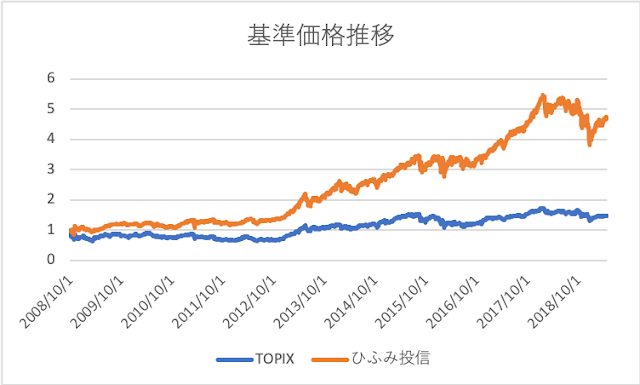
当該期間中、ひふみ投信の基準価格は4.70倍(純リターン371%)に、TOPIXは1.47倍(純リターン47%)になっています。
ひふみ投信の方が当該期間中の利殖幅が大きいという結果になりました。
ひふみ投信の対TOPIX超過収益率
ひふみ投信の対TOPIX超過収益率\( r_t^E\)は、ひふみ投信の日次リターン\( r_t^H\)とTOPIXの日次リターン\( r_t^T\)を用いて
r_t^E=r_t^H-r_t^T
\end{split} \]
ひふみ投信の対TOPIX超過収益率\( r_t^E\)は、ひふみ投信をロング、TOPIXをショートするポートフォリオのリターンに近似し、ひふみ投信がTOPIXをどれだけアウトパフォームしているかを測る指標になります。
ひふみ投信の対TOPIX超過収益率\( r_t^E\)の平均は0.04%、標準偏差は0.01%でした。
超過収益率が正であったため、ひふみ投信はTOPIXに対して良好なパフォーマンスを上げているという結果になりました。
ひふみ投信の対TOPIXの勝率
ひふみ投信の対TOPIX超過収益率\( r_t^E\)が正の値であるとき、ひふみ投信はTOPIXを上回るリターンを実現させたことになります。
\( r_t^E\)が正のとき\( 1\)、負のとき\( 0\)を取る変数(勝敗変数)を\( t=1,2,\cdots,2590\)に対して計算し、和を取ることで、ひふみ投信のリターンがTOPIXのリターンを上回った日数をカウントできます。
こうして計算した結果、2,590日中、ひふみ投信がTOPIXを上回った日数は1,385日、割合にして53.5%でした。
2008/10/1から2019/4/26までを計算期間としたときの、ひふみ投信の対TOPIXの勝率は53.5%であり、勝敗が一様に確からしい時の確率\( \frac{ 1}{ 2}\)を上回る結果となりました。
ひふみ投信の対TOPIX勝敗変数の二項検定(正規分布近似)
ひふみ投信の対TOPIX勝率は上記計算によると53.5%であり、勝率トントン(\(\frac{ 1}{ 2} \))に近く、偶然\(\frac{ 1}{ 2} \)を少し超える勝率が記録されただけではないか、という疑問を持ちます。
そこで、ひふみ投信の対TOPIX勝率53.5%という数字が、統計学的に意味がある数字なのかを検証します。
ひふみ投信の対TOPIX勝敗変数は、ひふみ投信の対TOPIX勝率\( p\)をパラメタとする二項分布に従うと考えられます。
「\( p=\frac{ 1}{ 2} \)と仮定したとき、ひふみ投信の対TOPIX勝率の実際値53.5%がどれくらいの珍しさで起こったのか」を統計的に検証する方法を、仮説検定と言います。
\( p=\frac{ 1}{ 2} \)と仮定したとき、ひふみ投信がTOPIXに2,590日中1,385日勝った、という結果が生じる確率が小さければ、ひふみ投信がTOPIXに勝ったのは偶然ではない、と結論付けられます。
仮説検定の詳細は他の記事にゆずりますが、今回はひふみ投信の対TOPIX勝利日数を二項分布\(Bi(2590,p) \)として、帰無仮説:\( p=\frac{ 1}{ 2} \)、有意水準5%で検定を行います。
参考記事:25-2. 二項分布を用いた検定
ひふみ投信の対TOPIX勝利日数は帰無仮説\( p=\frac{ 1}{ 2} \)のもとでは、近似的に平均\( 2590p=\frac{ 2590}{ 2}\)、分散\(2590p(1-p) =\frac{ 2590}{ 4}\)の正規分布に従います。
ひふみ投信の対TOPIX勝利日数を基準化した統計量が1.96より大きいとき、帰無仮説は棄却され、ひふみ投信の対TOPIX勝率は\( \frac{ 1}{ 2}\)と有意に異なる、と結論付けることが出来ます。
統計量は
\frac{ 1385- 2590p}{ \sqrt{2590p(1-p)}}=3.54>1.96
\end{split} \]
ひふみ投信の対TOPIX勝率は\( \frac{ 1}{ 2}\)と有意に異なります。
つまり、ひふみ投信の勝率が53.5%であり、\( \frac{ 1}{ 2}\)より大きかったのは、統計的には偶然ではない、という結論が導けます。
まとめ
ひふみ投信の設定以来のデータを用い、基本統計量をTOPIXと比較しました。
また、日次の勝敗率を計算し、ひふみ投信がTOPIXに有意に勝っていることを確認しました。
本記事の分析は統計的手法に基づいてはいるものの、ひふみ投信の一側面しか見えていないというご意見もあろうかと思いますので、是非SNSで「こんな見方もある」といったコメントを頂けると嬉しいです。