ブートストラップ法の概要と株価リターン分布への応用

あるデータがよく知られた確率分布から発生していると仮定して行う統計分析を「パラメトリック法」と呼びます。

投資シミュレーションプログラムは株価リターンが正規分布に従うと仮定しているため、「パラメトリック法」による分析です。
>>「投資シミュレーションプログラム」サマリー

しかし、データがよく知られた確率分布から発生しているとはみなせない場合には、無理やり何らかの確率分布に当てはめると、誤った結論を導くことになります。

したがって、あらかじめ確率分布を特定化せずに、確率分布を推定する方法を考えなければなりません。

その方法の一つが「ブートストラップ法（ブーツストラップ法）」です。

ブートストラップ法は、すでに得られているデータから無作為抽出を繰り返し、それを新たなデータとみなすことにより、確率分布や密度関数の推定を行ったり、標本平均や標準偏差といった統計量を計算する手法のことです。

ブートストラップ法は「データはこの確率分布から発生しているはずだ」という前提をおかず、「データをありのままに利用する」という考え方に基づいており、このような統計手法を「ノンパラメトリック法」といいます（厳密には、パラメトリックなブートストラップ法もあります）。

また、データをランダムに利用するという意味で、モンテカルロ法の一種とも言えます。

ブートストラップ法によれば、株価リターンのデータから、無作為にデータを抽出し、新たなデータとして扱うことになります。

これにより、リターンが正規分布に従うと仮定できなくても、実際の株価リターンデータを乱数のように用いて、統計的・確率論的な分析が可能になります。

実際に、日本株式のリターンを使って、分析を行ってみましょう。

まず、下記の記事を参考に、日本株式のリターンのデータを読み込みます。
>>ファーマ-フレンチの3ファクターモデルのデータを入手する方法

#csvデータの読み込み
JP <- read.csv("Japan_3_Factors_Daily.csv", skip=5)
#時系列データとして加工
JP_mkt<-ts(JP$Mkt.RF+JP$RF,start=JP$X[1])/100

日本株の日次リターンの統計量を求めてみます。

#平均
m=mean(JP_mkt)
#標準偏差
s=sd(JP_mkt)

library(moments)
#歪度：正規分布が0
skewness(JP_mkt)
skewness(rnorm(10000,m,s))
#尖度：正規分布が3
kurtosis(JP_mkt)
kurtosis(rnorm(10000,m,s))

株価リターンと同じ平均、標準偏差をもつ正規分布より、尖度はかなり大きな値になっていることがわかります。

データが正規分布に従うかを調べるための、コルモゴロフ・スミルノフ検定も行っていますが、「正規分布に従う」という帰無仮説は棄却され、株価リターンは正規分布ではないと結論付けられます。

#コルモゴロフ・スミルノフ検定
ks.test(JP_mkt, "pnorm", mean=m, sd=s)

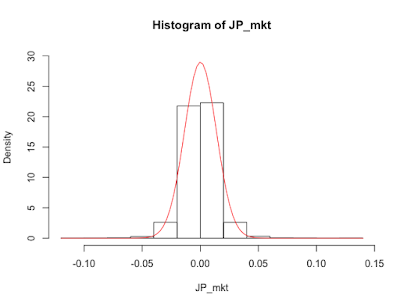
ヒストグラムを正規分布と比較してみます。実際の株価リターンデータと、同じ平均、標準偏差の正規分布の密度関数を描きます。実際のデータのほうが、左右の裾が厚い感じがします。

hist(JP_mkt,freq = FALSE,ylim=c(0,30))
curve(dnorm(x,m,s),add=TRUE,col="red")

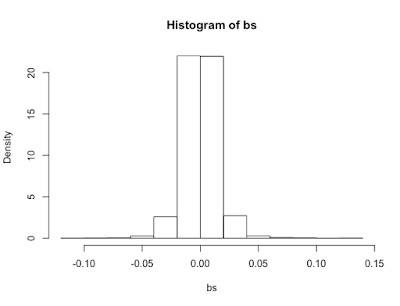
株価リターンにブートストラップ法を適用してみます。株価リターンから、無作為に10000個のサンプルを抽出し、ヒストグラムを描きます。
#ブートストラップ法

bs<-sample(JP_mkt,10000,replace=T)
hist(bs,freq = FALSE)

ブートストラップ法で得たサンプルを使って、損失確率を計算し、正規分布の場合と比較してみましょう。

#損失確率ブートストラップ法
length(bs[bs<0])/length(bs)
#損失確率正規分布
pnorm(0,m,s)

ブートストラップ法で得たサンプルから計算した損失確率は49.2%、正規分布の場合は49.5%でしたので、実際のデータのほうがやや損失が出にくい（利益が出やすい）分布であることがわかりました。

損失確率を求めるくらいであれば、データをそのまま使えばよいので、ブートストラップ法を適用する必要もありませんが、より複雑な分析をするときには、ブートストラップ法は強力なツールになります。

ブートストラップ法の概要と、株価リターン分析への応用可能性について説明しました。

実際の株価リターンは、理論で前提とするような正規分布ではありませんが、だからといって理論の価値が損なわれるわけではありません。

正規分布との差異をきちんと把握し、必要ならば適切に対処できることが大事です。
>>理論・モデルの意義と、理論と現実の差異を知ったあとにとるべき行動