【君の知らない複式簿記6】矢印簿記で仕訳をビジュアライズ

この記事では複式簿記における仕訳を矢印で表現する矢印簿記についてお話します。

矢印簿記では、仕訳に登場する勘定の繋がりを矢印で表現するので、複式簿記を直感的に理解するのに役立ちます。

まさに「仕訳をビジュアライズ」する方法です。

矢印簿記のアイデア

矢印簿記の考え方は単純です。矢印簿記では、ある仕訳を一つの矢印として表現します。貸方科目を始点、借方科目を終点とする矢印が、仕訳に対応します。

具体例を見てみましょう。

例題1.固定資産1000を現金で購入した

この仕訳は、貸方「現金」勘定から借方「固定資産」勘定への矢印として、次のように表せます。

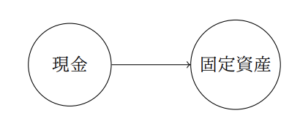
仕訳を矢印で表現する際に、借方の勘定を左に置かなくてはいけない、というようなルールは設けません。勘定科目の位置関係は関係なく、単に始点と終点と矢印の関係にのみ着目します。また、仕訳の金額も（とりあえず）無視します。

例題2.200の減価償却を行った

この仕訳は、貸方「減価償却累計額」勘定から借方「減価償却」勘定への矢印として、次のように表せます。

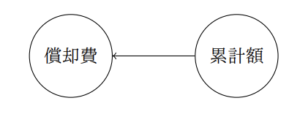
例題3.上記の固定資産を売却し、代金は来月回収することにした

この仕訳はやや複雑です。例題1.と2.のように、仕訳の貸借に勘定が1つずつ現れるような仕訳に分解しても良いですが、ここではシンプルに、貸方「固定資産」勘定・「固定資産売却益」勘定から、借方「未収金」勘定・「減価償却累計額」勘定への矢印として、次のように表すことにします。

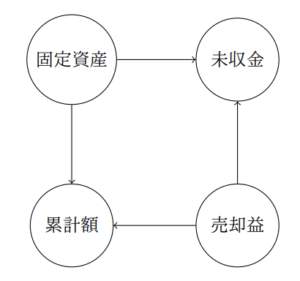
以上の3つの例をすべて組み合わせると、以下のような矢印の図が描けます。

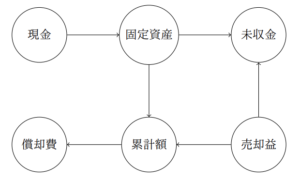
仕訳は矢印で表す矢印簿記をイメージしていただけたでしょうか。

複式簿記の有向グラフ

以上のような図式を有向グラフといいます。グラフとは、頂点の集合と頂点同士を結ぶ辺をセットにしたものです。各辺に向きがついているもの（つまり辺を矢印で表せるグラフ）を有向グラフといい、向きがついてないものを無向グラフといいます。

矢印簿記とは、複式簿記の有向グラフ表現とも言えます。

バランスベクトルとの関係

仕訳はベクトルとして表せます。ベクトル表示した仕訳をバランスベクトルといいます。

【参考記事】【君の知らない複式簿記4】簿記代数の教科書『Algebraic Models For Accounting Systems』とバランスベクトル

バランスベクトルと有向グラフはどんな関係にあるのでしょうか。再び例題を使って考えてみましょう。

例題1.固定資産1000を現金で購入した

この取引を表すバランスベクトルは以下のようになります。

このバランスベクトルの要素について、その符号のみに着目してみます。つまり、固定資産「1000」を固定資産「+」（プラス：借方）、現金「-1000」を現金「-」（マイナス：貸方）と考えると、

バランスベクトルのタイプが分かれば、有向グラフを作るのは簡単です。「-」の要素から「+」の要素への矢印を描けばよいのです。

例題2.200の減価償却を行った

この取引を表すバランスベクトルのタイプは

例題3.上記の固定資産を売却し、代金は来月回収することにした

「-」の要素から「+」の要素への矢印を描けば、有向グラフが得られます。

以上のように、有向グラフはバランスベクトル（のタイプ）がわかれば作ることが可能です。

矢印簿記の応用

矢印簿記に関する研究のなかには、日本語で読めるものいくつか存在します。雑誌『企業会計』の以下の記事は大変参考になります。

• 2017年1月号「クラウド会計が切り開く取引記録分析の可能性」椎葉
• 2020年8月号「タイムリーな情報を可視化する」椎葉・村上
• 2021年1月号~（連載）「会計，数理科学と出会う」椎葉

「矢印簿記」という呼び名は、椎葉先生からご教示いただいたものです。

これらの記事でも指摘している通り、矢印簿記は試算表から期中の取引を推定する道具として使うことが可能です。ある勘定から別の勘定に至る経路がいくつも存在するような有向グラフでは、期中の取引を推定するのが困難になるといった性質があることがわかっています。

Arya et al.の論文”Inferring Transactions from Financial Statements” では、矢印簿記と線形代数を用いて、財務諸表から取引を推定する手順を提示しています。

このように矢印簿記は会計情報を理解するのに役立てることができるのです。

また、有向グラフという数学的な姿を得たことで、複式簿記を幾何学の対象として捉えることも期待できます。幾何学的な議論によって、まだ私たちが知らない複式簿記の側面を見つけることができるかもしれません。このような分野は「簿記幾何」「簿記トポロジー」とも呼べるもので、個人的に興味を持っています。

【参考記事】簿記幾何・簿記トポロジーへの展望

この記事では仕訳の借方・貸方に登場する勘定から有向グラフを作り、その金額の情報は使いませんでした。それでは会計情報としての仕訳の意味合いを十分に反映できるとは言えません。仕訳の金額を考慮した有向グラフに関する研究も、今後進んでいくことでしょう。