この記事ではセミオートマトンとオートマトンの定義について解説します。
荒っぽく言えば、セミオートマトンとは入力によって変化する機構、オートマトンとは入力によって変化し、同時に出力も行う機構です。
本記事ではさらに、オートマトンと会計システムの関係についても触れます。
セミオートマトンの定義
セミオートマトンとは、2つの空でない集合\( Z,X\)と関数
\delta:Z\times X\to Z
\end{split} \end{equation}
\( Z\)を状態集合、\( X\)を入力文字集合、\( \delta\)を\( \mathcal{S}\)の状態遷移関数といいます。
セミオートマトンは次のような規則で「変化」するような機構です。セミオートマトンが状態\( z\in Z\)にいるとき、入力シンボル\( x\in X\)を読み込むと、状態は\( \delta(z,x)\in Z\)に移ります。
セミオートマトンの状態変化は、次のような矢印の図式で表せます。以下の図式は状態\( z\)にあるセミオートマトンが入力\( x\)を受け取って、状態\( z’\)に遷移したことを示しています。
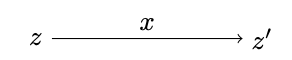
オートマトンの定義
オートマトンは、直感的にはセミオートマトンに出力を備えたものです。
オートマトンとは、セミオートマトンの三つ組\( \left( Z,X,\delta\right)\)に加え、空でない集合\(Y \)と関数
\lambda:Z\times X\to Y
\end{split} \end{equation}
\( Y\)を出力文字集合、\( \lambda\)を出力関数といいます。
オートマトンはセミオートマトンと同様に「変化」します。セミオートマトンと異なるのは、出力を伴う点です。
オートマトンが状態\( z\)にいるとき、入力シンボル\( x\)を読み込むと、状態は\( \delta(z,x)\)に移ります(ここまではセミオートマトンと同様)。これと同時に、オートマトンは出力シンボル\( \lambda(z,x)\in Y\)を出力します。
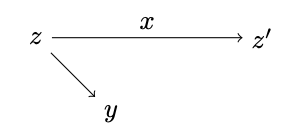
オートマトンの状態変化と出力も矢印の図式で表せます。以下の図式は状態\( z\)にあるオートマトンが入力\( x\)を受け取って状態\( z’\)に遷移し、その際に出力\( y\)を行ったことを示しています。
複式簿記への応用
オートマトンは会計システムをモデル化する際に使えます。
会計システムの状態はバランスベクトルとして表すことができ、取引が起こると(仕訳が入ると)状態が変化します。その際に、会計システムに関する情報を出力します。
会計システムをこのように表現すると、会計システムはまさにオートマトンであるといえるのです。
以下の参考文献では会計システムをオートマトンとして表し、その性質を研究しています。
参考文献
このブログで不定期連載中の【君の知らない複式簿記】では、簿記の代数構造に関する研究結果を紹介しています。
【君の知らない複式簿記】シリーズはこちらからどうぞ。