【君の知らない複式簿記 補遺】隣接行列とマテシッチの行列簿記

この記事では、グラフ理論に登場する隣接行列を紹介します。隣接行列は「簿記の行列表現」に用いられます。

その定義のと複式簿記への応用例について見ていきましょう。

【君の知らない複式簿記】シリーズの他の記事は__こちら__からどうぞ。

グラフ理論

この世界におけるさまざまな「つながり」「ネットワーク」は、グラフとして表せます。

グラフとは、頂点と辺からなる図のことです。

各辺に向きがついているとき有向グラフといい、各辺に向きがついていないグラフを無向グラフといいます。

SNSにおけるフォロー・フォロワーの関係は有向グラフとして表現できます。

複式簿記の仕訳に登場する借方・貸方の勘定科目の関係も有向グラフとして表現できます。

これらグラフを数学的に表し、その構造や効果を調べる分野を、グラフ理論といいます。

隣接行列(adjacency matrix)

隣接行列はグラフ理論に登場する正方行列です。

（有向・無向）グラフを行列で表現したものが隣接行列です。\( n\)個の頂点をもつグラフから、\( n\times n\)隣接行列が作られます。

グラフ内の2つの頂点を\( i,j\)としましょう。頂点\( i\)と\( j\)の間に辺があるとき、隣接行列の\( \left( i,j\right)\)成分と\( \left( j,i\right)\)成分を\(1 \)で、頂点\( i\)と\( j\)の間に辺がないとき\(0 \)で表すことで、グラフの「つながり」を行列によって表現できます。

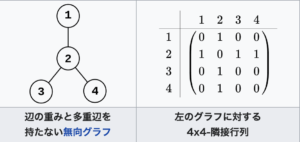
（画像出典 :Wikipedia 隣接行列）

辺に「重み」の情報が付与されている場合には、辺で結ばれた2つの頂点に対応する隣接行列の成分に（\( 1\)ではなく）その重みを入力することで、重み付きグラフの隣接行列も作ることが出来ます。

有向グラフでは「どの頂点からどの頂点に向かう辺なのか」が重要な情報です。これを表すために、頂点\( i\)から\( j\)への辺（矢印）があるときに隣接行列の\( \left( i,j\right)\)成分を\(1 \)（もしくは辺の重み）とし、逆向きの矢印がなければ\(\left( j,i\right)\)成分を\(0 \)とすることで、有向グラフの隣接行列が得られます。

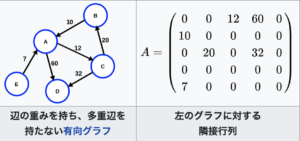
（画像出典 :Wikipedia 隣接行列）

無向グラフの隣接行列は対称行列ですが、有向グラフの隣接行列は一般に対称行列にはなりません。

マテシッチの行列簿記と隣接行列

マテシッチの行列簿記は隣接行列です。

マテシッチの行列簿記とは、仕訳の借方・貸方を行・列に対応付ける表現方法です。この方法で作成される行列（マテシッチ行列とよびます）は、勘定数×勘定数の正方行列の各要素に正数を配置して作成されます。各要素は仕訳の金額を意味しています。

たとえば、以下のような仕訳と行列の対応関係があります。

このマテシッチ行列は「資産」勘定を始点、「費用」勘定を終点とする、重み\( x\)の有向グラフと解釈することも出来ます。

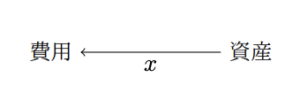
以上のことから、マテシッチ行列は隣接行列の一種であるといえます。

なお、仕訳にはその逆行列を考えることができます。上記仕訳の逆行列とその行列表現は、以下のようになります。

上記2つの行列の和は

この行列は仕訳

複式簿記を行列で表す方法はマテシッチ行列だけではありません。グラフ理論において登場する「接続行列(incidence matrix)」を用いた、別の行列表現もあります。そちらについては以下の記事をご覧ください。

【君の知らない複式簿記6】矢印簿記で仕訳をビジュアライズ

参考文献

接続行列はネットワーク（webページのリンクや人間関係など）を表すのに用いられ、研究対象になっています。下記書籍は接続行列を基礎としてネットワーク上の物理現象（波や熱の伝わり）を分析し、それをSNSの「炎上」の分析と関連付けるなど、面白い題材を扱っています。

マテシッチの行列簿記はいわゆる「行列簿記」として有名なものです。以下の書籍は行列簿記の歴史、実務への活用例、会計システムとの関係などについて論じており、大変興味深いです。

行列簿記についてはこちらの記事でも解説していますので、ご覧ください。

【君の知らない複式簿記1】行列簿記の意義、性質、限界