【君の知らない複式簿記 補遺】シェアーによる借方・貸方の説明と矢印簿記

100年前の会計研究者シェアーは、複式簿記の貸方借方について、「貸方は出発点、借方は到達点」であると説明しました。

実はこの表現、このブログでも取り上げた、矢印簿記の説明ととても良く似ています。

本記事では複式簿記の始点・終点としての貸方借方、そして矢印簿記との関係性について解説します。

この記事で考察するシェアーの主張は、下記の書籍 上野(2019)から引用しています。

シェアーの借方・貸方の説明

上野(2019)第1章は、19世紀の会計学者シェアーの学説から始まります。シェアーは簿記の教育者であり、簿記の構造の研究者でした。

シェアーは簿記を「資本循環の歴史記述」と位置づけました。ここで資本とは事業開始当初の純財産と、企業活動によってもたらされたその増減を指します。

資本を構成する積極財産（資産）と消極財産（負債）は、交換や変形によってさまざまに変化（転化）し循環します。複式簿記はその循環というある種の「運動」の様子を記録する機構です。

シェアーは複式簿記の基本概念である貸方借方を以下のように説明しています。

個々のすべての転化過程は，ある形態の財が他の形態の財に変化することであって，出発点と終着点等を有する運動である。すべてこれらの運動の出発点は，ある勘定の貸方であり，目標および終着点は，他の勘定の借方である

なかなか難しい表現ですが、ごく簡単に言えば「企業の活動を複式簿記で表すとき、貸方は出発点、借方は終着点を意味する」といったところでしょうか。

この「貸方は出発点、借方は終着点」という表現は、矢印簿記につながっていきます。

矢印簿記の復習

矢印簿記は、ある仕訳を矢印で表現する、複式簿記の一形態です。矢印簿記では、貸方科目に対応する頂点から、借方科目に対応する頂点に向けた矢印として、仕訳を表現します。仕訳の有向グラフによる表現、とも言い換えられます。

例えば「固定資産1000を現金で購入した」という取引を考えてみます。この取引を仕訳で表現すると

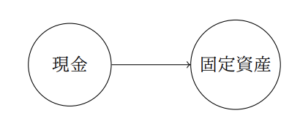
○で囲われた勘定科目の位置関係は気にしません。「現金」勘定と「固定資産」勘定の2つの○が左右逆でも、「現金」から「固定資産」に向けて矢印が惹かれていれば問題ありません。あくまで仕訳を「貸方科目から借方科目への矢印」で表すことが重要です。

シェアーの貸方借方の説明と矢印簿記の整合性

シェアーの主張は「出発点は貸方、終着点は借方である」という内容でした。これはまさに矢印簿記のルール「貸方科目から借方科目への矢印」と完全に整合しています。

貸方科目を出発点（始点）、借方科目を終着点（終点）とすると、その間を結ぶ矢印が引けます。シェアーの説明はまさに、複式簿記のビジュアル的に表現したものと言えるでしょう。

シェアーが矢印簿記や有向グラフをイメージしていたかは、定かではありません。少なくとも上野(2019)では矢印簿記に関する言及は見られません。

また、出発点・終着点という言葉は、必ずしも仕訳の貸借科目のことを指しているわけでもありません。むしろシェアーは財産勘定と資本勘定に関する貸借という、より大局的な構造の話を強調したかったと思われます。

しかし、シェアーの著書で述べられた「貸方始点、借方終点」という表現はまさに、現代において注目される矢印簿記の基本ルールそのものなのです。

シェアーの著書は1922年発刊、実に100年前の本です。その時代から変わらず認識される「仕訳の向き」に関する考え方は、複式簿記の本質の一つなのかもしれません。

参考文献

本記事では以下の書籍の第1章「シェアーの物的二勘定学説」を参考にしました。こちらの書籍は、600余年の歴史をもつ複式簿記の理論学説の中から、歴史的に特に重要なものを解説しています。いわゆる学術書ですが、興味がある方はきっと楽しめるでしょう。

矢印簿記については、こちらの記事に詳しく解説していますので、ご覧ください。
【君の知らない複式簿記6】矢印簿記で仕訳をビジュアライズ

その他の【君の知らない複式簿記】シリーズはこちらからどうぞ。