1. ホーム /
  2. 2019年 5月

2019年 5月 の投稿一覧

仮想通貨の価格ヒストリカルデータを取得する方法｜Rライブラリcryptoの使い方

こんにちは、毛糸です。

仮想通貨に再び注目が集まっています。

2017年に価格が高騰し、2018年に暴落した仮想通貨は、現代のバブルとして一躍有名になりました。
参考記事：ビットコインはバブルである

仮想通貨に関しては、その価格変動の激しさから、投機の対象ともなっていますが、適切にリスク管理しないとあっという間に資産が溶けてしまいます。
本記事では再び注目が集まっている仮想通貨に関して、統計プログラミング言語Rによる価格データの簡単な取得方法について解説します。

仮想通貨パッケージcryptoをインストールする方法

Rはライブラリと呼ばれるプログラム・パッケージを利用することで、専門的な分析を簡単に行えるようになります。
仮想通貨の価格分析をするにあたっては、cryptoパッケージが役に立ちます。
cryptoパッケージに内蔵されている関数を用いることで、仮想通貨の価格情報を簡単に取得できます（公式マニュアルPDFはこちら）。
cryptoパッケージを利用するにはお使いのPCにRがインストールされている必要がありますので、下記を参考にして環境を整えてください。

仮想通貨価格の時系列データ（ヒストリカルデータ）の入手方法

まずはじめに、cryptoパッケージ（と付随して必要な他のパッケージ）をインストールします。
Rのコンソール画面に以下のコードを入力し実行します。
install.packages("crypto", dependencies = TRUE)
しばらくの間、各種パッケージのインストールが進みます。
インストールが進んだら、cryptoパッケージを読み込みます。
library(crypto)
これでcryptoパッケージに内蔵される各種関数が使用可能になりました。
たとえば、仮想通貨のリストを入手するには、以下のコードを実行します。
#仮想通貨のリストを表示
crypto_list()
出力結果は以下のようになります。
> #仮想通貨のリストを表示
> crypto_list()
# A tibble: 2,212 x 6
   symbol name     slug      rank exchange_url                history_url                           
   <chr>  <chr>    <chr>    <dbl> <chr>                       <chr>                                 
 1 BTC    Bitcoin  bitcoin      1 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 2 ETH    Ethereum ethereum     2 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 3 XRP    XRP      ripple       3 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 4 BCH    Bitcoin… bitcoin…     4 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 5 EOS    EOS      eos          5 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 6 LTC    Litecoin litecoin     6 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 7 BNB    Binance… binance…     7 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 8 BSV    Bitcoin… bitcoin…     8 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
 9 USDT   Tether   tether       9 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
10 XLM    Stellar  stellar     10 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/…
# … with 2,202 more rows

ビットコイン（BTC）の価格データからリターンとリスクを計算する

実際にデータを分析してみましょう。

ヒストリカルデータの取得

crypto_history()関数で、指定した仮想通貨の時系列価格情報を取得できます。
#crypto_history(coin = NULL, limit = NULL, start_date = NULL
#end_date = NULL, coin_list = NULL, sleep = NULL)
#仮想通貨の価格等情報を取得
#dateはyyyymmdd形式で。NULLとすると最長期間
BTC<-crypto_history(coin = "BTC",
                    start_date = NULL,end_date = NULL)
日付を指定することで、特定期間のデータを取得することも出来ます。
BTC_saikin<-crypto_history(coin = "BTC",
              start_date = "20190501",end_date = "20190530")
head()関数、tail()関数で、データの先頭と最後尾を確認できます。
#データの先頭
head(BTC,1)
#データの最後尾
tail(BTC,1)
crypto_history()で取得される情報は、時点の情報や始値、終値など、いくつかの列から構成されています。
それぞれの情報にアクセスしたければ、たとえばBTC$closeのように$マークのあとに取り出したい列のラベルを指定します。

終値を時系列データとして抽出

今回使うのはBTCの終値closeです。関数ts()にデータを入れることで、時系列（time series)データとして扱うことが出来ます。
#BTCの終値情報を時系列として取り出す。
#時系列情報の開始日をBTC$date[1]と指定
BTC_price<-ts(BTC$close,start=BTC$date[1])

価格チャート

BTC価格のチャートを描いてみます。データの図示にはplot()関数を使います。
#type="l"は線グラフ
plot(BTC_price,type="l")

BTCの日次収益率（リターン）

日次収益率を計算します。
t日目のBTC価格を\( P_t\)、収益率を\( r_t\)と表すと、
\[ \begin{split}r_t=\frac{ P_{t}-P_{t-1}}{ P_{t-1}} \end{split} \]
と計算できます。
分子は1時点前との差額を計算するdiff(_,lag=1)関数、分母は1時点前の価格を返すlag(_,k=-1)関数を用いて計算できますので、BTCの日次収益率は以下のようにして求めます。
#日次収益率
BTC_return_daily<-diff(BTC_price,lag=1)/lag(BTC_price,k=-1)
plot(BTC_return_daily,type="l")

BTCリターンの平均と標準偏差（リスク）

日次収益率の平均はmean()関数を用いて計算できます。
mean(BTC_return_daily)*100
#[1] 0.2808807
#表示は%
#年率換算では
mean(BTC_return_daily)*100*365
#[1] 102.5215
BTCの日次平均リターンは0.28%(年率換算102%)でした。この値はデータ期間によって変わります。

標準偏差はsd()関数で計算できます。

sd(BTC_return_daily)*100
#[1] 4.333606
#表示は%
sd(BTC_return_daily)*100*365^0.5
#[1] 82.79343
リスクを示す標準偏差は日次で4.33%、年率換算82.79%でした。極めてハイリスクです。

まとめ

Rパッケージcryptoを用いて仮想通貨の価格を用意に取得できることを説明しました。
今後このデータを用いて、仮想通貨に関する統計分析をシリーズでお送りする予定です。
もし面白いと思っていただけたら、SNSでのシェアをよろしくお願いします。

「投資シミュレーションプログラム」サマリー（随時追加）

こんにちは、毛糸です。

本記事は「投資シミュレーションプログラム」に関する記事のまとめページです。

「投資シミュレーションプログラム」とそれを使った各種の分析について、このページから各記事に飛ぶことが出来ます。

投資シミュレーションプログラム

投資シミュレーションプログラムVer.1.0

投資シミュレーションプログラムVer.1.0のコード例と、投資シミュレーションプログラムが用いている「モンテカルロ・シミュレーション」に関する説明は下記ページです。
>>投資シミュレーションプログラムを作ってみた【Rでプログラミング】

投資シミュレーションプログラムVer.1.1

投資シミュレーションプログラムは何千何万という膨大な数のシナリオをコンピュータの圧倒的計算力で処理するプログラムですが、Ver.1.0ではサンプルの計算をfor文を用いて行っていました。

統計プログラミング言語Rはfor文による繰り返し計算よりベクトル演算の方が高速に処理することができ、これを実装したのがVer.1.1です。
>>投資シミュレーションプログラムを高速化してみた

活用例

年金の分析

投資シミュレーションプログラムを用いて、年金積立金のポートフォリオの将来予測を行っています。積立金の100年後の状況を予測したり、1年後に損失が生じる確率が35%あることなどが明らかになりました。
今後、運用期間中に資金が出入りするような、より現実的な仮定のもとで分析を行う予定です。

FX・外貨預金の分析

FXの期待リターンの理論値を計算したうえで、それをパラメタとして投資シミュレーションプログラムを使い、FXで億り人になれる確率や破産する確率を計算しました。

レバレッジが億り人になれるキーであることが明らかになりましたが、破産確率の上昇と隣合わせであることもわかりました。
>>FXの期待リターン、億り人になれる確率、破産する確率【モンテカルロ・シミュレーション】

インデックス投資の分析

資産運用の王道、インデックス投資について、投資シミュレーションプログラムを用いた将来予測を行う予定です。

投資シミュレーションプログラムを支える技術

投資シミュレーションプログラムは、3つの技術と知識によって支えられています。
  1. 確率論・統計学
  2. ファイナンス理論（金融工学）
  3. プログラミング言語
投資シミュレーションプログラムは、確率論における「大数の法則」によって正当性が保証される「モンテカルロ・シミュレーション（モンテカルロ法）」により、将来の予測値を計算しています。
分析の対象は投資であり、金融商品です。金融商品の性質や運用戦略の策定については、ファイナンス（金融工学）の分野において知見が蓄積されています。
投資シミュレーションプログラムにおける実際の計算はコンピュータが行いますので、必然的にプログラミングのスキルが必要になります。投資シミュレーションプログラムは統計プログラミングRを用いて作成されています。
ファイナンスにおけるモンテカルロ法の活用については、下記の書籍が大変役に立ちます。

統計プログラミング言語Rによるファイナンス分析に関しては、下記書籍を読めば、Rの基本的な使いかたから、本格的な分析までを学ぶことが出来ます。

 

投資シミュレーションプログラムを高速化してみた

こんにちは、毛糸です。

先日、投資の将来予測を行うためのRプログラム「投資シミュレーションプログラム」を公開しました。
>>投資シミュレーションプログラムを作ってみた【Rでプログラミング】

このプログラムを用いて、年金の将来予測を行ったり、FXで億り人になれる確率を計算したりしました。

>>将来の年金積立金の状況と損失確率をシミュレーションしてみた【モンテカルロ・シミュレーション】

>>FXの期待リターン、億り人になれる確率、破産する確率【モンテカルロ・シミュレーション】

「投資シミュレーションプログラム」を使ってみる中で、より「速く」計算するための改善策を思いついたのでメモしておきます。

本記事では投資シミュレーションプログラム1.1（2019年5月29日現在の最新版）の内容を説明します。

Rプログラムを速くするための方法：ベクトル化

統計プログラミング言語Rは、ベクトル演算を高速で行える言語として知られています。

ここではベクトルを「数値やモノ（オブジェクト）を並べたもの」と理解しておけば十分です。

ベクトル演算が高速で行える、とは、具体的には、for文などを用いて一つ一つの対象（オブジェクト）を順繰りに処理していくよりも、ベクトルというまとまりに対して一括で処理を行うほうが速い、ということです。

投資シミュレーションプログラムでは、乱数をサンプル数×年数の数だけ発生させ、

  1. あるサンプルについて、各年の資産額をfor文で計算して
  2. その処理をサンプル数の数だけfor文で繰り返す
という、2重のfor文構造になっています。
しかし、Rはfor文よりもベクトルとして計算したほうが速いため、for文をベクトル演算で置き換えれば、高速化が可能なのです。

投資シミュレーションプログラムのベクトル化

投資シミュレーションプログラムは、年ごとに資産額を計算し、それをサンプルの数だけ繰り返すという方法をとっています。
このうち、年ごとの計算については、前年の資産額に収益率を乗じて当年の資産額を算出しているため、年ごとに資産額を計算する必要があり、for文を使うことを回避できません。
しかし、サンプル数分の繰り返しについては、サンプル一つ一つを順繰りに計算するのではなく、これをベクトル化してやることで、for文を回避することが可能です。

下記に示す投資シミュレーションプログラム1.1は資産額をベクトル化して計算することで、サンプルの繰り返し計算を回避しています。

#投資年数（自由入力）
Year<-40
#シミュレーション回数（自由入力、多いほど正確だが時間がかかる）
sample<-100000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)
#初期投資額を入力（自由入力）
initial<-2000
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#期待リターン（期待収益率μ、自由入力）
mu<-7/100
#リスク（標準偏差σ、自由入力）
sigma<-12.88/100
#シミュレーション開始
#sampleの計算は明示せずベクトル化
for ( t in 1:Year){
    #今年の資産額=前年の資産額*(1+収益率)
    A[,t+1]<-A[,t]*(1+rnorm(sample,mu,sigma))
}
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の期待値は",mean(A[,Year+1]))

投資シミュレーションプログラム1.0と1.1の処理時間の比較

ベクトル化によりどれくらい高速化されたのか検証してみましょう。

R onlineでは実行時間が自動計測されますので、これを利用します（手持ちのPCで実行する場合はtitocライブラリを使ったりsystem.timeを使ってください）。

サンプル数100,000(10万)回のシミュレーションで、for文を使って計算するVer.1.0と、ベクトル演算を行うVer.1.1を比較すると、以下のようになりました。

投資シミュレーションプログラムVer.1.0（for文による繰り返し計算）

Absolute running time（絶対実行時間）は、17.18秒でした。

投資シミュレーションプログラムVer.1.1（ベクトル演算）

Absolute running time（絶対実行時間）は、1.46秒でした。

Ver.1.0からVer1.1に改善した場合の処理速度は1/10以上に縮まりました、驚異的な改善です。

まとめ

Rというプログラミング言語はベクトル演算を得意としており、for文をベクトル演算に書き換えられれば大幅な効率化に繋がります。

「動けばOK」という段階から一歩進んで、より速いプログラムを目指したいと思います。

本記事は、以下の書籍を参考にしました。Rを用いたデータ分析や投資意思決定に役立つ知識が豊富に紹介されており、とてもおすすめです。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”ファイナンスのためのRプログラミング証券投資理論の実践に向けて”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/41UrHrQ9vlL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%8A%E3%83%B3%E3%82%B9%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AER%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E2%80%95%E8%A8%BC%E5%88%B8%E6%8A%95%E8%B3%87%E7%90%86%E8%AB%96%E3%81%AE%E5%AE%9F%E8%B7%B5%E3%81%AB%E5%90%91%E3%81%91%E3%81%A6%E2%80%95-%E5%A4%A7%E5%B4%8E-%E7%A7%80%E4%B8%80/dp/4320110447″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”mcwYY”});

将来の年金積立金の状況と損失確率をシミュレーションしてみた【モンテカルロ・シミュレーション】

こんにちは、毛糸です。

先日発表された金融審議会市場ワーキング・グループの報告書案「高齢社会における資産形成・管理」（以下「報告書案」、外部リンク）は、老後に年金を頼り生活するという前提を否定するかのような内容と受け取られ、話題になっています。

この報告書案を読まれた方の中には「年金なんてこれからどんどん給付額が減っていくから当てにならない！」と考えている方もいらっしゃるでしょう。

実際に将来の給付額がどうなるかというのは、人口動態や賃金・物価上昇率など、多くの要因に左右されるため、現時点で確定的なことを述べることは出来ません。

しかし、年金積立金の運用という観点から、金融データと確率論に基づき年金ポートフォリオの将来をシミュレーションすることは可能です。

本記事では年金積立金の基本ポートフォリオに関する将来予測を、モンテカルロ・シミュレーションに基づいて行ってみたいと思います。
参考記事：投資シミュレーションプログラムを作ってみた【Rでプログラミング】

本記事をお読みいただくことで、将来の年金積立金がいくらになるのか、そのリスクはどのくらいか、年金運用が損失を出す確率はどのくらいかといった情報を知ることが出来ます。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”[参考文献]ファイナンスのためのRプログラミング証券投資理論の実践に向けて”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/41UrHrQ9vlL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%8A%E3%83%B3%E3%82%B9%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AER%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E2%80%95%E8%A8%BC%E5%88%B8%E6%8A%95%E8%B3%87%E7%90%86%E8%AB%96%E3%81%AE%E5%AE%9F%E8%B7%B5%E3%81%AB%E5%90%91%E3%81%91%E3%81%A6%E2%80%95-%E5%A4%A7%E5%B4%8E-%E7%A7%80%E4%B8%80/dp/4320110447″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”YwNTV”});

年金積立金の基本ポートフォリオ

私たちが毎月支払っている年金保険料は、年金積立金管理運用独立行政法人(GPIF)という機関によって運用が行われています。

GPIFは年金支払のための原資を効率的に運用するため、株式や債券などのリスク資産に投資を行っています。

GPIFは年金ポートフォリオとして

  • 国内債券
  • 国内株式
  • 外国債券
  • 外国株式
の4つの資産クラスに投資を行うことを取り決めており、その割合も決まっています。以下はGPIFのサイト「基本ポートフォリオの考え方」（サイト）からの引用です。

この「基本ポートフォリオ」は、賃金上昇率+アルファを確保しつつ、リスクを最小限にして運用されることを目的としており、期待リターンは年4.75%、標準偏差で測ったリスクは年12.8%となっています。
参考記事：年金のリスクとリターンを統計プログラミング言語Rで計算してみた

今回はこのデータをもとに、将来の年金がどのくらいの規模になるのか、損失が出る確率はどのくらいなのかを計算してみたいと思います。

年金ポートフォリオのモンテカルロ・シミュレーション

年金積立金ポートフォリオが将来いくらくらいになるのか予測してみましょう。

年金運用の期待リターンは年4.57%、標準偏差で測ったリスクは年12.8%として、毎年の投資収益率が正規分布に従うと仮定した場合に、将来の年金ポートフォリオの金額を乱数を用いて予測します。

シミュレーションには「投資シミュレーションプログラム」を使います。
参考記事：投資シミュレーションプログラムを作ってみた【Rでプログラミング】

投資年数Yearは、1年、25年、50年、100年を入力し、それぞれの年数経過後の資産額をシミュレーションします。

投資の期待リターンはGPIFの基本ポートフォリオの期待リターン4.57%(4.57/100)を、投資のリスクは基本ポートフォリオのリスク（標準偏差）12.8%(12.8/100)を入力します。

#期待リターン（期待収益率μ、自由入力）
mu<-4.57/100
#リスク（標準偏差σ、自由入力）
sigma<-12.8/100

以下では1年後、25年後、50年後、100年後の将来における年金積立金の期待値と、標準偏差で測ったリスク、当初資金を下回る確率（損失確率）、損失が発生した場合の平均損失額（これを期待ショートフォールとよびます）を計算します。

なお、シミュレーションにあたって分析を単純化するために、運用以外の資金の出入りはないものとし、リバランスは考慮しないものとします。また、当初資金は記事執筆時点直近で報告された運用額である150兆6,630億円（150.6630兆円）とします。

1年後の年金のシミュレーション結果

  • 1年後の年金積立金の期待値は157兆円
  • 標準偏差で測ったリスクは19兆円
  • 損失確率は35%
  • 損失発生時の平均損失額（期待ショートフォール）は13兆円
1年後に損失が発生する確率が35%もあるのは驚きですが、損失が発生してもその期待値は13兆円なので、あまり大きな額ではありません。

25年後の年金のシミュレーション結果

  • 25年後の年金積立金の期待値は467兆円
  • 標準偏差で測ったリスクは313兆円
  • 損失確率は6%
  • 損失発生時の平均損失額（期待ショートフォール）は32兆円

25年後には年金積立金の期待値は現在の倍以上になります。

50年後の年金のシミュレーション結果

  • 50年後の年金積立金の期待値は1,422兆円
  • 標準偏差で測ったリスクは1,476兆円
  • 損失確率は2%
  • 損失発生時の平均損失額（期待ショートフォール）は39兆円
50年後に損失が発生する確率は2%であり、50年に一度と言われるような金融危機が起こらない限りは発生し得ないレベルです。

100年後の年金のシミュレーション結果

  • 100年後の年金積立金の期待値は13,389兆円
  • 標準偏差で測ったリスクは25,865兆円
  • 損失確率は0.2％
  • 損失発生時の平均損失額（期待ショートフォール）は52兆円
100年後に損失を抱える確率はほぼゼロです。

まとめと考察

投資シミュレーションプログラムを用いて、長期の年金運用の成績を予測してみました。
投資年数が長くなるほど将来の資産額の期待値は大きくなることがわかりましたが、一方でリスクも大きくなるようです。
年金運用で損失が出る確率は運用が長期になるほど低くなりますが、来年損失が出る確率は35%もあり、25年程度の運用でも6%の確率の確率で運用損が生じることもわかりました。
年金制度の将来を占うにあたり、今回の分析はやや設定を単純化しすぎていますが、たとえば今後年金運用が損失を出すようなことがあっても「統計的にはまぁ損失もありうるよね」と納得する材料にはなるのではないでしょうか。
年金制度はその存続も含め、今後も議論になるものと思われますが、多角的な視点から考えてみたいと思います。
なお、本記事の分析を行うに際して、下記の書籍を参考にしました。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”ファイナンスのためのRプログラミング証券投資理論の実践に向けて”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/41UrHrQ9vlL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%8A%E3%83%B3%E3%82%B9%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AER%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E2%80%95%E8%A8%BC%E5%88%B8%E6%8A%95%E8%B3%87%E7%90%86%E8%AB%96%E3%81%AE%E5%AE%9F%E8%B7%B5%E3%81%AB%E5%90%91%E3%81%91%E3%81%A6%E2%80%95-%E5%A4%A7%E5%B4%8E-%E7%A7%80%E4%B8%80/dp/4320110447″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”S6AUW”});

FXの期待リターン、億り人になれる確率、破産する確率【モンテカルロ・シミュレーション】

こんにちは、毛糸です。

資産運用にはいろいろな手段があり、なかでも外貨預金やFX（外国為替証拠金取引）は有名どころです。

しかし、外貨預金やFX（以下FX等といいます）は、文献によっては「手を出すべきでない」投資商品として紹介されていたりもします。

たとえば『図解・最新　難しいことはわかりませんが、お金の増やし方を教えてください！』には、以下のように説明されています。

『為替が上がるか、下がるか』と、『金利が高いか、安いか』をセットで考えて、取引価格が決まっているから、買う前にどっちの通貨がお得かは言えない

外貨預金をやるのはコイントスで『表』か『裏』にお金をかけるのとほぼ一緒

 

本記事ではこの主張について詳しく掘り下げ、FX等の期待リターンについて考察したあと、それに基づく「億り人になれる確率」と「破産する確率」を投資シミュレーションプログラムを用いて計算してみます。

外貨預金・FXはなぜ魅力的なのか

FX等は、2つの収益機会にあずかれます。

ひとつは海外通貨に対して適用される高い金利収入（インカムゲイン）、もうひとつは通貨高による価値の増加（キャピタルゲイン）です。

外貨預金は通常、高金利通貨建てで設定され、高い金利収入（インカムゲイン）が得られるとされています。

またキャピタルゲインに関しても、例えば米ドル建て外貨預金をするとして、1ドル100円のときに1万ドルを預金し、引き出し時に1ドル110円になっていれば、円建てでは100万円から110万円に増えることになります。

FXも同様に、為替の変動による利益を得つつ、スワップポイントと呼ばれる金利収入が得られます。

このように、インカムゲインとキャピタルゲインが同時に得られるという魅力があるため、FX等は人気の投資となっています。

FXリターン分析の前提①：裁定取引とフォワード・パリティ

FX等の期待リターンについて考察する前に、いくつかテクニカルな前提をおきます。

今後、通貨高が見込めるような通貨があったとしましょう。つまり、キャピタルゲインが見込めそうな通貨です。

為替の世界には、将来の為替レートを現時点で「約束」する契約が存在します（通貨先物や為替予約といいます）。

もし将来、通貨高になりそうな通貨に対して、将来低いレートで買う「約束」をすることができれば、その取引を行う投資家は、将来安いレートで通貨を買い、高い市場レートで売却することで利益が得られそうです。

このような投資家の行動を「裁定」とよび、通貨は投資家の裁定によって「適正水準」に収斂します。

やや数学的な表現をすると、将来の( T)年後のスポット為替レートの期待値\(E[S_T] \)が「約束」されたフォワード為替レート\( F_T\)と異なっていれば、市場の効率性を前提として裁定が行われ、両者は一致するようにレートが変化します。つまり

\[ \begin{split} F_T=E[S_T]\end{split} \]
という等式が成り立つようにフォワード為替レート\( F_T\)が調整されます。

両辺を現在のスポット為替レート\( S_0\)で割ると

\[ \begin{split} \frac{ F_T}{S_0 }=E[\frac{ S_T}{ S_0}]=E[1+s_{0,T}]\Leftrightarrow E[s_{0,T}]=\frac{ F_T}{S_0 }-1\end{split} \]
となります。\(E[s_{0,T}] \)は為替の変化率（純額表示のキャピタルゲイン）です。

この等式をフォワード・パリティとか、為替レートの期待形成条件といいます。

 

FXリターン分析の前提②：カバー付き金利パリティ

さて、FX等で高金利通貨を買うことで、高いインカムゲインが得られ、運が良ければキャピタルゲインにもあずかれます。

しかし、このような目論見はあらゆる市場参加者（個人投資家や、証券会社などの機関投資家）が狙っているものです。

もし高い金利水準にありながら割安な通貨があれば、その通貨にはまたたく間に買いが入り、一瞬で「適正水準」にまで通貨高になります。

そうなれば、将来のキャピタルゲインの幅が縮まって、投資の旨味が小さくなりますので、投資家は早くに将来の為替レートを「約束」しようとします。

こうした取引によって、フォワード為替レートで「約束」した通貨の値上がり益は、最終的には金利差と同じ水準になるよう調整されます。

数式で表すと、スポット為替レートを\( S_0\)、フォワード為替レートを\( F_T\)、売り通貨の金利（国内金利）を\( i_D\)、買い通貨の金利（海外金利）を\( i_F\)としたとき

\[ \begin{split} \frac{ F_T}{S_0 }=\frac{1+i_D}{ 1+i_F}\simeq 1+i_D-i_F \end{split}\]
という関係が成り立ちます（右辺は近似式）。

つまり、フォワード為替レートという「約束」された為替レート（カバーされたレート）で測る通貨のリターンは、内外金利差と一致するということです。

FX等の期待リターンはゼロ

フォワード・パリティとカバー付き金利パリティを組み合わせると、FX等の期待リターンが計算できます。

FX等の期待リターンは、金利差（インカムゲイン\( i_F-i_D\)）と通貨高による増分（キャピタルゲイン\( E[s_{0,t}]\)）の和を意味します。

フォワード・パリティより

\[ \begin{split}E[s_{0,T}]=\frac{ F_T}{S_0 }-1 \end{split} \]
であり、

カバー付き金利パリティより

\[ \begin{split}\frac{ F_T}{S_0 }-1\simeq i_D-i_F  \end{split} \]
ですから、これらを合わせると
\[ \begin{split}E[s_{0,T}]= i_D-i_F \Leftrightarrow (i_F-i_D)+E[s_{0,T}]=0\end{split} \]
となります。第一項はインカムゲイン、第二項はキャピタルゲインを表しており、これらの和、つまりFX等の期待リターンは０であることが示されました。

以上のことをまとめると、フォワード・パリティとカバー付き金利パリティによって、FX等の期待リターンは、インカムゲインとキャピタルゲインが相殺され０になる、ということです。

以上の内容は、下記書籍により詳しい説明と数式での証明が載っていますので、合わせてご参照ください。

FXで億り人になれる確率、破産する確率

期待リターンが0のFXで十分な資産を築ける確率はどれくらいなのでしょうか。

以下では当初資金1,000万円をドル円（年あたりリスク１０％と想定）で運用するとして、10年後に億り人になれる確率と破産する確率を計算します。

FXはレバレッジ取引が可能ですから、レバ1倍、5倍、10倍のそれぞれのケースを考えてみます。

本性の計算は「投資シミュレーションプログラム」を用いています。シミュレーション回数は10000回です。

  1. レバ1倍の場合、10年後の資産の期待値は1,002万円、億り人になれる確率は0%、破産する確率は0%
  2. レバ5倍の場合、10年後の資産の期待値は1,018万円、億り人になれる確率は1.5%、破産する確率は20%
  3. レバ10倍の場合、10年後の資産の期待値は1,866万円、億り人になれる確率は3.12%、破産する確率は83%

考察

期待リターン0のFXでは、レバをかけないと億り人にはなれないことがシミュレーションで明らかになりました。
また、レバを高めることで億り人になれる確率は高まりますが、同時に破産する確率も高くなることがわかりました。

まとめ

フォワード・パリティとカバー付き金利パリティという関係式から、FX・外貨預金は理論上、期待リターンが0であることがわかりました。この前提のもとで投資を行うと、レバレッジをかけないと多大な富を築くことは出来ないことが明らかになりましたが、一方で破産の確率も高まることがわかりました。

本記事の内容は複数の仮定に基づくものであり、実際の投資収益の成否を保証するものではなく、また実際にFX等で成功していらっしゃる方々の成果を否定する意図は全くありません。また、シミュレーションはあくまで確率論に基づいた予測であることをお断りしておきます。

 

【投信定点観測】11週目｜ファーウェイ・ショック

こんにちは、毛糸です。

【投信定点観測】2019年5月第4週（スタートから11週目）の損益の報告です。

今週末における投資総額は156万円、含み損益は-13,892円、損益率は-0.89%（年率-2.89％）です。

損益状況

商品ごとの時価は以下のようになりました。【投信定点観測】開始から11週間経過時の含み損益は-13,892円で、先週から11,714円のマイナスです。

損益率に直すとこんな感じです。今週末の損益率は-0.89%（年率換算で-2.89％）です。

年率換算の損益率の計算式が誤っていたので、今回修正しました。

インデックス投資信託の振り返り：株式総崩れとREIT続伸

株安が止まりません。

中国通信機器メーカーファーウェイが米国市場から閉め出されるというニュースが報じられ、同社と取引のある企業の株価が下落。その不安感が相場全体に広がり暗雲が立ち込めています。

先進国株式は今週-2.16%の下落、中国を含む新興国株式も-2.80%の下落と大きなダメージです。

他方、J-REITは更に上昇し、週間+1.34%の伸びです。都市圏のオフィス需要が高水準で推移し、世界的な金利低下の流れが追い風となり、資金流入が続いているようです。

株式市場全体が悲観的なムードですが、【投信定点観測】で実践するインデックス投資は、市場の短期的な上げ下げに惑わされずに投資を続けていくことで、市場全体の成長を享受する方法です。

市場全体が下げているときは、裏を返せば安く資産を購入できるチャンスでもあります。

好景気になってから投資するのでは遅いので、是非このタイミングでインデックス投信の積立投資を初めてみてください。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”お金は寝かせて増やしなさい”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51xHIGALUZL.jpg”,”/51UFsW4HuvL.jpg”,”/51d7m7hcbYL.jpg”,”/61ULYpbutcL.jpg”,”/51uCgEZrhmL.jpg”,”/51ne7%2Bl4ysL.jpg”,”/51TjKtJWpzL.jpg”,”/51Zj-OmTSML.jpg”,”/410JAnn80uL.jpg”,”/51cjtS6tWPL.jpg”,”/61Q0Zvqja7L.jpg”,”/613B004TKQL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%8A%E9%87%91%E3%81%AF%E5%AF%9D%E3%81%8B%E3%81%9B%E3%81%A6%E5%A2%97%E3%82%84%E3%81%97%E3%81%AA%E3%81%95%E3%81%84-%E6%B0%B4%E7%80%AC%E3%82%B1%E3%83%B3%E3%82%A4%E3%83%81/dp/4894517833″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″}});

ロボアドバイザーの振り返り：THEO（テオ）とWealthNavi（ウェルスナビ）のリスク

ロボアドバイザーのTHEO（テオ）は今週-0.43%(含み損益-1.70%)、WealthNavi（ウェルスナビ）は今週-1.37%(含み損益-2.01%)でした。

【投信定点観測】を開始して11週目ということで、両者のリスク（リターンの標準偏差）を算出してみたところ、

  • WealthNaviのリスクは1.70%/週
  • THEOのリスクは1.59%/週
でした。
含み損益率ベースではWealthNaviの方が高いので、いまのところTHEOの方がローリスク・ローリターンであるといえます。
▼ロボアドバイザーTHEO（テオ）は登録はこちらから！
THEO

▼ロボアドバイザーWealthNavi（ウェルスナビ）の登録はこちらから！

WEALTHNAVI（ウェルスナビ）

アクティブファンドの振り返り：ひふみとセゾン、明暗分かれる

日本株式に投資するアクティブファンドとして、【投信定点観測】ではひふみ投信とセゾン資産形成の達人ファンドに投資しています。

現状、両者の明暗ははっきりしており、セゾン投信のパフォーマンスの高さが圧倒的です。

両者のリスク（リターンの標準偏差）を算出してみたところ、

  • セゾン資産形成の達人のリスクは2.10%/週
  • ひふみのリスクは1.90%/週
となっており、ひふみの方がローリスク・ローリターンです。

アクティブファンドはインデックスを上回る超過収益を得ることを目的としており、今の所、その目標は達成できていますので、今後の運用結果がたのしみです。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”いま選ぶべきアクティブ投信この8本!”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/51yqlV5edSL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%84%E3%81%BE%E9%81%B8%E3%81%B6%E3%81%B9%E3%81%8D%E3%82%A2%E3%82%AF%E3%83%86%E3%82%A3%E3%83%96%E6%8A%95%E4%BF%A1%E3%81%93%E3%81%AE8%E6%9C%AC-%E4%B8%AD%E9%87%8E-%E6%99%B4%E5%95%93/dp/4534056877″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”stdO3″});

まとめ

【投信定点観測】を始めて11週、市場は冷え込み続けており、投資パフォーマンスは悪化しています。

投資初期では良好な成績を収めていた株式が、一転大きく毀損しており、特定の資産クラスに資金を集中させることの恐ろしさを実感します。

投資信託は手軽に分散投資が行える優れた金融商品ですが、市場全体の変動にはどうしてもつられてしまいます。

そんな状況であっても、異なる変動性を持つ別の資産クラスに広く投資することで、資産全体の変動性を抑えることが可能です。

複数の資産クラスに分散することをアセット・アロケーション（資産配分）といいますが、投資成果の大部分はこのアセット・アロケーションによって決まるとも言われています。

アセット・アロケーションの重要性は以下の書籍でも強調されています。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”お金は寝かせて増やしなさい”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51xHIGALUZL.jpg”,”/51UFsW4HuvL.jpg”,”/51d7m7hcbYL.jpg”,”/61ULYpbutcL.jpg”,”/51uCgEZrhmL.jpg”,”/51ne7%2Bl4ysL.jpg”,”/51TjKtJWpzL.jpg”,”/51Zj-OmTSML.jpg”,”/410JAnn80uL.jpg”,”/51cjtS6tWPL.jpg”,”/61Q0Zvqja7L.jpg”,”/613B004TKQL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%8A%E9%87%91%E3%81%AF%E5%AF%9D%E3%81%8B%E3%81%9B%E3%81%A6%E5%A2%97%E3%82%84%E3%81%97%E3%81%AA%E3%81%95%E3%81%84-%E6%B0%B4%E7%80%AC%E3%82%B1%E3%83%B3%E3%82%A4%E3%83%81/dp/4894517833″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″}});

引き続き積立投資の状況をリポートして参りますので、もしよろしければSNSでのシェアよろしくお願い致します！

投資シミュレーションプログラムを作ってみた【Rでプログラミング】

こんにちは、毛糸です。

投資にはリスクがあります。

自分の資産が将来どれくらいの金額になるのか、リタイアまでにどれくらいの資産を築けるのか、といった疑問に、現時点で確定した答えを出すのは不可能です。

しかし、投資データと統計学を用いて、将来をシミュレーションすることは可能です。

私は大学院で金融工学を専攻し、公認会計士として日々数字と向き合う仕事をしながら、プログラミングを勉強して投資意思決定に使えるツールを開発して遊んでいます。

今回はそんな日々の勉強の成果として「投資シミュレーションプログラム」を作ってみました。

将来に渡って投資を行っていった場合に、数年・数十年後にいくらの資産が築けるかをシミュレーションするプログラムです。

この記事では「投資シミュレーションプログラム」のコードをすべて公開し、その使いかたを解説します。

統計プログラミング言語Rと、オンラインでの利用

統計プログラミング言語Rは、データサイエンスで用いられるプログラミング言語です。

統計解析や計算を簡単に行うことができ、計算機としても使えます。

本記事ではプログラミング言語Rを用いて、投資シミュレーションプレミアムを作成します。

Rを使うには、本来RのソフトウェアをPCにインストールする必要がありますが、今回はちょっとした計算に使うのみなので、ブラウザ上で完結するR onlineを利用します。
参考記事：ブラウザ上でRプログラミング（R online、Rオンラインを使う方法）

R onlineのサイト（リンク）でコードを打ち込めば、すぐにRによる計算が実行できます。

試しにサイト上で
1+1
と入力し、[Run it]してみると、すぐに下の方に計算結果が表示されます。

以下、このR onlineを使って、「投資シミュレーションプログラム」作成します。

すでに打ち込んである内容は、すべて削除して構いません。

投資シミュレーションプログラムの流れとモンテカルロ・シミュレーション

「投資シミュレーションプログラム」は、以下のような流れでシミュレーションを行い、将来の投資額の予測値や確率分布を算出します。
  1. 投資のリターンやリスクなどの前提条件を入力する
  2. 時間ステップ（年単位、日単位など）ごとに「乱数」を発生させ、ランダムな収益率をシミュレーションする
  3. 複利計算により将来の資産額を算出する
  4. 以上を数千、数万回繰り返し、確率論的に将来資産額の推定値を算出し確率分布を予測する
このように、乱数を用いて将来を予測しシミュレーションする方法を「モンテカルロ・シミュレーション（モンテカルロ法）」といいます。

モンテカルロ・シミュレーションは金融実務において非常に重要な手法として認知されており、金融機関においてデリバティブの価格計算やリスク管理などに用いられています。

「投資シミュレーションプログラム」はモンテカルロ・シミュレーションを使って、将来の資産額がどれくらいになるかを予測するプログラムです。

「投資シミュレーションプログラム」のコードは以下にすべて記しており、コードをR onlineにコピー＆ペーストするだけでシミュレーションを行うことが出来ます。

モンテカルロ法は統計学・確率論を基礎として、プログラミング言語を用いながら、ファイナンスの知識をフル活用する高度な手法です。下記書籍はそんなモンテカルロ法を基礎から学べる良書ですので、気になる方は是非手にとってみてください（本書が理解できれば投資シミュレーションプログラムはゼロから自作できます）。


インプット情報の入力

まず、シミュレーションに必要な情報を入力します。

投資年数を入力します。以下では年単位で入力することとし、40年間の投資をシミュレーションしてみますが、自由に変更して構いません。

#投資年数（自由入力）
Year<-40

シミュレーション回数を入力します。今回シミュレーションに使用するのは金融工学で用いられる「モンテカルロ法」という手法で、統計学の「大数の法則」に従っています。シミュレーション回数が多いほど「正確な」計算ができますが、計算に時間がかかるようになります。100回や1000回程度だと、シミュレーションの都度、結果がばらつきます。

#シミュレーション回数（自由入力、多いほど正確だが時間がかかる）
sample<-10000

「投資シミュレーションプログラム」では毎年のリターンが確率的に決まるような状況で、資産額がどのように変化するかをシミュレーションするものです。そのために、シミュレーションの数値を格納する「箱」を用意し、ここに数値を格納します。「箱」は数学用語でいうところの行列にあたります。

#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)

初期投資額を入力します。投資元本（元手）は自由に決めて構いません。単位も問いません（今回は2000万円のつもりで2000を入力します）。

#初期投資額を入力（自由入力）
initial<-2000

先ほど作成したシミュレーション数値格納用の「箱」に初期投資額を代入します。

#シミュレーション数値に初期投資額を入力
A[,1]<-initial

投資の期待リターンを入力します。ここでは一年あたりの期待収益率を入力します。今回は投資の年あたり期待リターンを7%として計算します。

#期待リターン（期待収益率μ、自由入力）
mu<-7/100

投資のリスクを入力します。今回は米国株式に連動して値動きする投資信託VTIのリスク（標準偏差）としての概算値12.88%(12.88/100)を入力します（参考ページリンク）。

#リスク（標準偏差σ、自由入力）
sigma<-12.88/100

「投資シミュレーションプログラム」では、各年の投資収益率が既に入力したリターンとリスクに基づいた正規分布に従うと仮定し、正規分布に従う確率変数（乱数）を多数発生させて将来を予測します。Rではrnorm()で正規分布に従う乱数を生成することが出来ます。この正規乱数を、投資年数×シミュレーション回数の分だけ作ります。

#乱数を生成（ランダムな投資収益率）
x<-rnorm(sample*Year,mu,sigma)

次に、生成した乱数を計算に適した行列形式に整えます。

#乱数（ランダムな収益率）を行列形式に変換
z<-matrix(x,sample,Year)

ではシミュレーションを初めましょう。シミュレーションはsample回行います。各シミュレーションにおいて、1年ごとに資産額を算出します。今年の資産額=前年の資産額×(1+収益率)で計算できます。この計算をRのfor文（繰り返し文）を用いて行います。

#シミュレーション開始
for (s in 1:sample){
        for ( t in 1:Year){
            #今年の資産額=前年の資産額*(1+収益率)
            A[s,t+1]<-A[s,t]*(1+z[s,t])
        }
}

シミュレーションの結果、つまり投資期間経過後の資産額はA[,Year+1]という「箱」に収められています。

シミュレーションでは、良い投資結果を収めたシナリオもあれば、ほとんど儲からなかったケースもあります。全体的な「傾向」を知るためには、シミュレーション結果の平均や中央値を計算します。

#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の期待値は",mean(A[,Year+1]))
#シミュレーション結果の中央値を表示
paste(Year,"年後の資産額の中央値は",median(A[,Year+1]))

投資期間経過後の資産額はA[,Year+1]に格納されていますので、ここから将来の資産額の分布を用いた様々な確率の計算が可能です。

たとえば将来の資産額が初期投資額を下回るような確率（つまり投資で損失が発生する確率）も計算できます。

#損する確率を表示
paste("損失を被る確率は",length(A[,Year+1][A[,Year+1]<initial])/sample)
ヒストグラムを描くことで、将来の資産額の確率分布をビジュアル的に知ることも出来ます。
#将来の資産額の確率分布（ヒストグラム）を表示
hist(A[,Year+1])

この結果は乱数を用いたものなので、このプログラムを走らせるたびに結果が変わります。乱数の変動性を取り除きたい（つまりより高い精度で計算したい）場合は、sampleの数を増やしてください。

今回の例では、年あたりの収益率が期待リターン7％、リスク（標準偏差）12.88％の正規分布に従うような投資機会に、当初一括で2,000万円を投資した場合に、40年後の資産額の期待値が約3億円となることがわかりました。

まとめ

モンテカルロ・シミュレーションで将来の資産額を推計する「投資シミュレーションプログラム」を作成しました。
以下がそのコードの全体像です。
#投資年数（自由入力）
Year<-40
#シミュレーション回数（自由入力、多いほど正確だが時間がかかる）
sample<-10000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)
#初期投資額を入力（自由入力）
initial<-2000
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#期待リターン（期待収益率μ、自由入力）
mu<-7/100
#リスク（標準偏差σ、自由入力）
sigma<-12.88/100
#乱数を生成（ランダムな投資収益率）
x<-rnorm(sample*Year,mu,sigma)
#乱数（ランダムな収益率）を行列形式に変換
z<-matrix(x,sample,Year)
#シミュレーション開始
for (s in 1:sample){
        for ( t in 1:Year){
            #今年の資産額=前年の資産額*(1+収益率)
            A[s,t+1]<-A[s,t]*(1+z[s,t])
        }
}
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の期待値は",mean(A[,Year+1]))
#シミュレーション結果の中央値を表示
paste(Year,"年後の資産額の中央値は",median(A[,Year+1]))
#損する確率を表示
paste("損失を被る確率は",length(A[,Year+1][A[,Year+1]<initial])/sample)
#将来の資産額の確率分布（ヒストグラム）を表示
hist(A[,Year+1])
このプログラムを使うことで、将来の資産額の推計につかったり、将来資産を10倍にするために必要なリターンを探したり、投資で損失が出る確率を知ってリスク管理に活かすことも出来ます。
今後このプログラムを更に発展させていきたいと思います。

もし「こんな使い方もできる！」「こんな内容も知れたらいいな」といったアイデアがあれば、是非教えてください！

参考文献

「投資シミュレーションプログラム」はモンテカルロ・シミュレーションという手法に基づく予測を行っております。モンテカルロ・シミュレーションを投資に活用するためには、統計学・プログラム・ファイナンスの知識が必要になりますが、下記書籍はそれらを必要な範囲で解説しており、優れた良書です。

プログラミング言語Rを使ってファイナンスや投資の問題を分析するテキストとして、下記が参考になります。

年金が「目標を達成できない確率」を統計プログラミング言語Rで計算してみた

こんにちは、毛糸です。

前回、年金ポートフォリオのリスクとリターンを、統計プログラミング言語Rを使って計算してみました。
参考記事：年金のリスクとリターンを統計プログラミング言語Rで計算してみた

今回は前回のコードを少し応用して、私たちの年金ポートフォリオが「目標を達成できない確率」を計算してみたいと思います。

年金運用の目標

私たちの年金資産の運用を所管する年金積立金管理運用独立行政法人（GPIF）は、私たちの年金が安定的かつ効率的に運用されるようなポートフォリオを組み、年金資産を運用しています。

「基本ポートフォリオの考え方」（外部リンク）に記載されている通り、2014年には年金運用の中期目標が見直され、以下のような考え方のもと運用が行われることとなりました。

年金積立金の運用は（中略）財政の現況及び見通しを踏まえ、保険給付に必要な流動性を確保しつつ、長期的に積立金の実質的な運用利回り（積立金の運用利回りから名目賃金上昇率を差し引いたものをいう。）1.7％を最低限のリスクで確保することを目標とし、この運用利回りを確保するよう、積立金の管理及び運用における長期的な観点からの資産構成割合（基本ポートフォリオ）を定め、これに基づき管理を行うこと。

ここに書いてあるとおり、年金運用は資産の運用利回り（リターン）から名目賃金上昇率を控除した実質的な運用利回りを1.7％確保することを目標としています。

本記事では統計プログラミング言語Rを用いて、年金運用がこの目標を達成できない確率を計算してみようと思います。

Rの使いかたに関しては前回の記事「年金のリスクとリターンを統計プログラミング言語Rで計算してみた」を参照するか、もしくはより深い理解をしたい方には、下記書籍をおすすめします。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”金融データ解析の基礎 (シリーズ Useful R 8)”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/41Nyynhmv5L.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E9%87%91%E8%9E%8D%E3%83%87%E3%83%BC%E3%82%BF%E8%A7%A3%E6%9E%90%E3%81%AE%E5%9F%BA%E7%A4%8E-%E3%82%B7%E3%83%AA%E3%83%BC%E3%82%BA-Useful-R-8/dp/4320123719″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”wjJhB”});

年金ポートフォリオと名目賃金上昇率

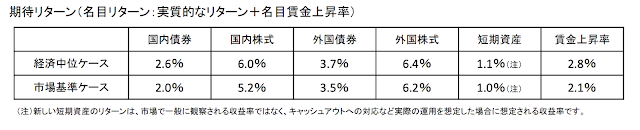
「基本ポートフォリオの考え方」（外部リンク）で提供されている「【参考資料】年金積立金管理運用独立行政法人の中期計画（基本ポートフォリオ）の変更（2014年10月31日）」[PDF：249KB]（以下の画像は断りがなければこちらからの引用です）には、年金ポートフォリオが投資する各資産の期待リターンと名目賃金上昇率が載っています。

Rに以下のように入力し、リターンと賃金上昇率のベクトル（期待リターンベクトル）を作成します。

#各資産クラスの期待リターン（実質、経済中位） 

mu<-c(2.6/100, 6.0/100, 3.7/100, 6.4/100, 1.1/100,2.8/100)

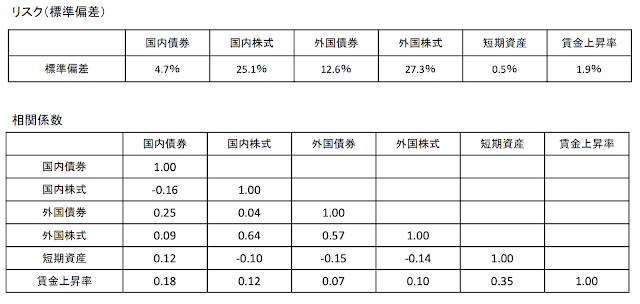
同様に、各資産と賃金上昇率のリスク（標準偏差）と相関についても、以下のように入力します。

#各資産クラスの分散（標準偏差の２乗） 

sigma<-c(4.7/100, 25.1/100, 12.6/100, 27.3/100, 0.5/100,1.9/100) 

#相関行列

Rho<-rbind(

     c(1,-0.16,0.25,0.09,0.12,0.18),

     c(-0.16,1,0.04,0.64,-0.1,0.12),

     c(0.25,0.04,1,0.57,0.15,0.07),

     c(0.09,0.64,0.57,1,-0.14,0.10),

     c(0.12,-0.1,-0.15,-0.14,1,0.35),

     c(0.18,0.12,0.07,0.10,0.35,1))

年金ポートフォリオの実質リターン

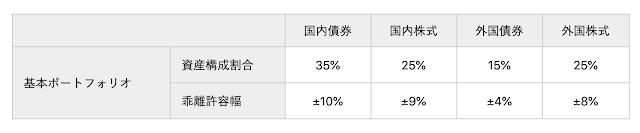
年金ポートフォリオは、以下のような資産配分で投資が行われます。
  • 国内債券（期待リターン(r_1 =2.6%)）に35%（これを( w_1)とおく）
  • 国内株式（期待リターン(r_2 =6.0%)）に25%（これを( w_2)とおく）
  • 外国債券（期待リターン(r_3 =3.7%)）に15%（これを( w_3)とおく）
  • 外国株式（期待リターン(r_4 =6.4%)）に25%（これを( w_4)とおく）
  • 短期資産（期待リターン(r_5 =1.1%)）に0%（これを( w_5)とおく）
このとき年金ポートフォリオの期待リターン(mu_{PF} )は

[ begin{split}
mu_{PF}=sum_{i=1}^5 w_i r_i
end{split} ]と書けます。

実質リターンはここから名目賃金上昇率（これを( r_w)とします）を差し引けばよいので、年金ポートフォリオの実質期待リターン( mu_{Real})は

[ begin{split}
mu_{Real}=mu_{PF}-r_w
end{split} ]となります。

Rではこれを以下のように記述します。

#ポートフォリオから名目賃金上昇率を控除する実質ポートフォリオのウエイト

weight_Real<-c(0.35,0.25,0.15,0.25,0,-1)

#ポートフォリオから名目賃金上昇率を控除した実質リターン

(mu_Real<-weight_Real%*%mu)

スポンサードリンク


(adsbygoogle = window.adsbygoogle || []).push({});

年金ポートフォリオの実質リスク（標準偏差）

同様に、リスク（標準偏差）についても計算します。

前回の記事「年金のリスクとリターンを統計プログラミング言語Rで計算してみた」と同じく、分散ベクトルと共分散行列から、分散共分散行列を作成します。

Rでは以下のように記述します。

#実質標準偏差
Var_Real<-weight_Real%*%Sigma%*%weight_Real
#ポートフォリオのリスク（標準偏差）
sigma_Real<-Var_Real^0.5
これでポートフォリオの実質リスク（標準偏差）が計算できました。

年金ポートフォリオの目標が達成できない確率と下方確率

各資産の収益率と賃金上昇率が、以上で述べたような期待リターンベクトルと分散共分散行列をもつ多次元正規分布に従うと仮定すると、年金ポートフォリオの実質収益率も正規分布に従うことがわかります。

正規分布の性質や計算方法について詳しく知りたい方は、下記参考文献を参照してください。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”統計学入門”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/512H1E9ARDL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E7%B5%B1%E8%A8%88%E5%AD%A6%E5%85%A5%E9%96%80-%E5%9F%BA%E7%A4%8E%E7%B5%B1%E8%A8%88%E5%AD%A6%E2%85%A0-%E6%9D%B1%E4%BA%AC%E5%A4%A7%E5%AD%A6%E6%95%99%E9%A4%8A%E5%AD%A6%E9%83%A8%E7%B5%B1%E8%A8%88%E5%AD%A6%E6%95%99%E5%AE%A4/dp/4130420658″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”A0r5B”});

年金ポートフォリオの実質リターン（名目リターンから賃金上昇率を控除したもの）を( r_{Real})とすると、( r_{Real})は平均( mu_{Real})、分散(sigma_{Real}^2 )の正規分布に従います。

したがって、年金ポートフォリオが目標となる実質利回り1.7%を達成できない確率( P(r_{Real}<1.7%))は、計算以下のように計算できます。

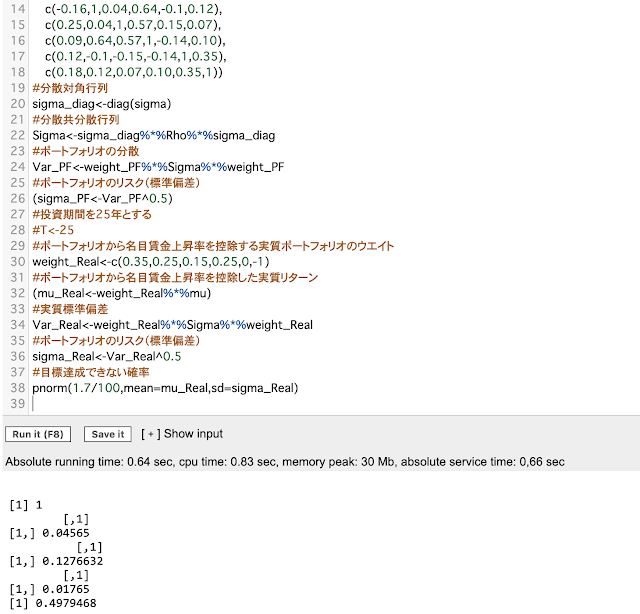
#目標達成できない確率
pnorm(1.7/100,mean=mu_Real,sd=sigma_Real)
結果は49.8%でした。
目標を達成できない確率が約半分というのはオカシイと思われるかもしれませんが、この目標は期待リターンが1.7%を上回るようなギリギリのラインとして設定されたものなので、こういう結果になって当然です。
なお、資料には名目リターンが賃金上昇率を下回る確率（下方確率）も記載されています。
こちらは実質利回り( r_{Real})が0以下となる確率( P(r_{Real}<0))を意味するので、以下のような計算で求められます。
#下方確率
pnorm(0,mean=mu_Real,sd=sigma_Real)

計算結果は0.444(44.4%)で、上記資料と一致しています。

この確率は名目リターンが賃金上昇率を下回る確率であり、運用によって給付の伸びを賄えない状況ということです。

まとめ

年金ポートフォリオが運用目標利回りである1.7%を超えられない確率は49.8%でした。

また、名目リターンが賃金上昇率に達しない確率（下方確率）は44.4％でした。

年金に関しては、最近金融庁が示した報告書でその制度の存続性に疑問が投げかけられており、議論の的となっています。
参考記事：【年金は頼れない？】「高齢社会における資産形成・管理」を読んだあとに私たちが取るべき行動

年金制度の今後について議論する際には、本記事のような科学的・数理的検知からの判断も考慮できるとよいのではないでしょうか。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”人生100年時代の年金戦略”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/513QJpUzziL.jpg”,”/51aYTRz-7LL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E4%BA%BA%E7%94%9F100%E5%B9%B4%E6%99%82%E4%BB%A3%E3%81%AE%E5%B9%B4%E9%87%91%E6%88%A6%E7%95%A5-%E7%94%B0%E6%9D%91-%E6%AD%A3%E4%B9%8B/dp/4532358027″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”dAsUD”});

【年金は頼れない？】「老後までに2,000万」報告書を読んだあとに私たちが取るべき行動

こんにちは、毛糸です。

2019年5月22日、金融審議会市場ワーキング・グループが「高齢社会における資産形成・管理」と題する報告書の案を公表し（以下「報告書案」、外部リンク）、話題になっています。

人生100年と言われる現代日本において、金融機関に対する顧客目線に立った資産管理のあり方に指針を提供する内容です。

報告書はまだ素案の段階ですが、ニュースメディアはこぞってこれを取り上げています。

なかには「実質的な年金制度の敗北宣言だ」と言わんばかりの取り上げ方をしているメディアもありますが、本当でしょうか？

今回はこの報告書案の内容と、私たちが取るべき行動について考えてみたいと思います。

忙しい人のための報告書案まとめ

まず、忙しい読者の方のために、「高齢社会における資産形成・管理」の内容を箇条書きでまとめてみました。
  • 高齢社会の金融サービスのあり方についてまとめている
  • 高齢化は進み続けており、「資産寿命」の長期化の重要性が増している
  • 老後を見据え現役時代から資産形成に取り組む必要があり、金融機関はそのニーズに応えることが求められる
  • 唯一の正解はないが、個々人がリテラシーを高め「自分ごと」として資産形成に取り組むべし
これらの内容に関連して、以下では補足的な情報と、私たちが取るべき具体的な行動について考えてみます。

超高齢社会の日本の現状

現代の日本は超高齢社会といわれ、総人口に占める高齢者（65歳以上）の割合は27.3%に登ります。

既に国民の4人に1人は高齢者なのです（内閣府高齢化の状況より）。

日本人の平均寿命は男性81歳女性87歳に達し、今後も医療の発展等によりさらに長寿化すると考えられています。

（出所：報告書案 p3）

そんな状況において深刻化するのがいわゆる「長生きリスク」です。

長生きすることで老後の生活費に困窮したり、医療・介護費を工面できなくなるなどのリスクが懸念されています。

今回の報告書案はそうした長生きリスクに対処すべく、資産寿命をいかに伸ばすかという観点から指針が示されたものです。

高齢期に備えた資産管理の必要性

報告書案では、老後までの資産形成について「かつてのモデルは成り立たなくなってきている」と指摘されており、退職金や国民年金・企業年金に依存してきた旧来の老後の資産形成のあり方に警鐘を鳴らしています。

報告書案には高齢無職世帯の平均値として毎月5万円の赤字になっていることが示されており、リタイア後の余生30年で約2,000万円の取り崩しが必要であると述べられています。

メディアではこの内容を受けて「年金を当てにせず自助に努めよという政府からのメッセージ」と捉える向きもあるようです。

報告書案では年金制度の破綻に関して直接述べられてはいないものの、「少子高齢化により働く世代が中長期的に縮小していく以上、年金の給付水準が今までと同等のものであると期待することは難しい」との記述があり、ネガティブな印象は拭いきれません。

国に任せていれば安心、という前提は、政府の打ち出す制作やメッセージに鑑みるともはや成り立たないと考えたほうがよく、資産形成について一人ひとりが責任を持って向き合う必要があります。

現役世代が利用すべき制度：NISAとiDeCo

個人の自助努力による資産形成の支援政策として、NISAとiDeCoがあります。

（出所：報告書案 p29）

これらは投資信託などの金融商品に対して行った投資について、運用益への課税が免除されたり、現役世代の税金が減るといったメリットがあります。

NISAもiDeCoも現役世代の資産形成の強い味方であり、私も最大限活用しています。

NISA、iDeCoは証券会社がこぞって解説をしている他、下記の書籍などにその内容や上手な利用方法がまとまっていますので、将来に向けて準備したい人は早めに勉強すると良いでしょう。

ハイリスク商品に注意、リテラシーを高めて

自助努力による資産形成の重要性が高まっているのは確かですが、一方で過度な恐怖心を持つのはかえって危険です。

年金が破綻する、老後の生活費の確保が難しくなる、といったフレーズは、金融機関からすれば、高い手数料を生むハイリスクな商品を買わせるチャンスでもあります。

老後の不労所得を確保するという建前で、収益性の低い不動産を高い価格で売ろうとしてくる業者も現れるでしょう。

大切なのは、自分の将来を可能な限り客観的に予測・評価し、過度な不安にとらわれることなく、自分自身で判断できるようなリテラシーを身につけることです。

もしこれを読んでいるあなたが自身の資産形成に全く興味を持っていなかったとしたら、今が絶好の機会だと思って、資産運用の入門書を手に取るなどしてみてはいかがでしょうか。

【疑うことはコスト】他人の仕事を疑う前に確認すべき5つのこと

こんにちは、毛糸です。

先日読んだ本『どこでも誰とでも働ける――12の会社で学んだ“これから”の仕事と転職のルール』に「疑うことはコストである」という考え方が述べられています。
相手の言うことをいちいち疑って確認をとっていたら、時間とコストがかかり、組織運営のスピードが失われます。
変化の激しい現代においてビジネスで勝ち残るためには、「疑うことはコスト」と考えて疑いを排除することで、迅速な意思決定をする必要があります。
とはいえ、自分が作業している中で、他者の仕事や成果物に疑義を抱いてしまう場面は多々あります。
今回はそういうシーンに出くわしたとき、他者を疑う前に確認すべき5つことについて、まとめてみたいと思います。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”どこでも誰とでも働ける12の会社で学んだこれからの仕事と転職のルール”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/413DbsWpjpL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%A9%E3%81%93%E3%81%A7%E3%82%82%E8%AA%B0%E3%81%A8%E3%81%A7%E3%82%82%E5%83%8D%E3%81%91%E3%82%8B%E2%80%95%E2%80%9512%E3%81%AE%E4%BC%9A%E7%A4%BE%E3%81%A7%E5%AD%A6%E3%82%93%E3%81%A0%E2%80%9C%E3%81%93%E3%82%8C%E3%81%8B%E3%82%89%E2%80%9D%E3%81%AE%E4%BB%95%E4%BA%8B%E3%81%A8%E8%BB%A2%E8%81%B7%E3%81%AE%E3%83%AB%E3%83%BC%E3%83%AB-%E5%B0%BE%E5%8E%9F-%E5%92%8C%E5%95%93-ebook/dp/B07BQVWMFF”,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”ZHRur”});

関連する文書やルールを確認する

企業には業務上のルールがあり、それを文書化している場合があります。
大企業であれば内部統制の観点から業務ルールが明文化されていることが通常です。
もし他者の仕事に疑わしい部分を見つけたら、まずその業務に関するルールや文書を確認しましょう。
もしかしたら、その疑いは自分の理解が不十分なことに由来しているかもしれません。
人を疑う前に、まずルールを確認し、あるべき業務がどういうものであるかを確かめましょう。

同じロジックで再実施する

他者の仕事の結果が疑わしい場合、同じ前提条件でもう一度作業を振り返ってみると、自分の思い過ごしや誤解が解けることがあります。
他者の仕事に何らかの疑義がある場合、それはヒューマンエラーであることもあれば、自分の知らない手続きをしているのかもしれません。
時間はかかりますが、可能な限りで同様のロジックで再実施することで、本当に他の人がミスをしているのか、それとも自分の勘違いやケアレスミスによるものなのかが判別できます。


(adsbygoogle = window.adsbygoogle || []).push({});

以前に同じ状況や類似例がないか確認する

他人の仕事の結果がいつもと違う場合や、不自然な点がある場合、以前に同じ状況が起こっていないか、類似の例がないかを確認しましょう。
ビジネス環境が目まぐるしく移り変わる現代とはいえ、ルーティンワークであれば全く新しい状況が頻発するようなことはそうそうありません。
もし他者の仕事に疑わしい部分や不明点があったら、同様の状況が以前にも起きていないかを確認し、類似の状況を探しましょう。
もし同じような状況が起きていれば、今回も同様に対処することで問題を解決できるかもしれません。

日を置いて再度考える

もし「これは上流工程の担当者のミスでは……」と疑わしい状況に出くわしても、すぐにその人を問いただすのは良い方法とは言えません。
相手は自分の仕事を否定されたと思ってしまいますし、確認のために手を止める必要が出てきます。
もしすでに述べたような確認を行ってもなお疑念が払拭できない場合は、いったん時間をおいて、再度考えてみることをおすすめします。
もちろん緊急の仕事の場合は聞いてしまったほうがよいかもしれません。
しかし、ある程度スケジュールにバッファがあるなら、日をおいてから再考することで、新しい着眼点が得られ、問題が解決できるかもしれません。

前任者・チェック担当者に相談する

もし自分自身では解決できないようであれば、前任者やチェック担当者（レビュアー）に状況を相談してみるのも良いでしょう。
もし自分が着任して間もないような場合や、業務の進め方や内容について理解が不十分な場合には、自分より理解のある人に相談すると、問題が解決できることがあります。
もちろんこの場合は、相談相手の時間を使ってしまうことになるので、歓迎はされないかもしれません。
しかし、十分な検討をしてなお解決できない場合には、より理解ある人に助けを求めることが、結局は効率的であったりもします。


(adsbygoogle = window.adsbygoogle || []).push({});

まとめ

変化の激しい現代において「疑うことはコスト」です。
しかし、他者の仕事に疑義を抱いてしまうような状況は完全には回避できません。
そんなときは、以下の5つを実践してみてみてください。
  1. 関連する文書やルールを確認する
  2. 同じロジックで再実施する
  3. 以前に同じ状況や類似例がないか確認する
  4. 日を置いて再度考える
  5. 前任者・チェック担当者に相談する
私はこれらの項目をチェックリストにして、何か困ったとにには必ず確認するようにしています。
参考記事：チェックリストで仕事が劇的に楽になった件

これらのことを確認をすることで他の人を疑わずに済めば、余計ないざこざを回避できますし、効率的な業務運営につながります。

むやみに人を疑う前に、まずは自分自身での解決を目指しましょう。

(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”どこでも誰とでも働ける 12の会社で学んだこれからの仕事と転職のルール”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/413DbsWpjpL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%A9%E3%81%93%E3%81%A7%E3%82%82%E8%AA%B0%E3%81%A8%E3%81%A7%E3%82%82%E5%83%8D%E3%81%91%E3%82%8B%E2%80%95%E2%80%9512%E3%81%AE%E4%BC%9A%E7%A4%BE%E3%81%A7%E5%AD%A6%E3%82%93%E3%81%A0%E2%80%9C%E3%81%93%E3%82%8C%E3%81%8B%E3%82%89%E2%80%9D%E3%81%AE%E4%BB%95%E4%BA%8B%E3%81%A8%E8%BB%A2%E8%81%B7%E3%81%AE%E3%83%AB%E3%83%BC%E3%83%AB-%E5%B0%BE%E5%8E%9F-%E5%92%8C%E5%95%93-ebook/dp/B07BQVWMFF”,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”8Vk07″});

Warning: Trying to access array offset on value of type bool in /home/r1406503/public_html/keito.luxe/wp-content/themes/xeory_base/lib/functions/bzb-functions.php on line 299

Warning: Trying to access array offset on value of type bool in /home/r1406503/public_html/keito.luxe/wp-content/themes/xeory_base/lib/functions/bzb-functions.php on line 301
class="col-md-4" role="complementary" itemscope="itemscope" itemtype="http://schema.org/WPSideBar">