こんにちは、毛糸です。
先日、会計×テクノロジーをテーマとした勉強会コミュニティPyCPAの『モンテカルロ法によるリアル・オプション分析』輪読会第1回が開催されました。
今回は20名近い参加者にお集まりいただきました。
本記事では今回の輪読会の振り返りをしてみたいと思います。
参加者には事前にアンケートにお答えいただいてますので、その結果もあわせて公開します。
PyCPAとは
PyCPAは、テクノロジーの進化を武器に次世代の担い手となる探求者たちのコミュニティです。
もともとは、プログラミング言語Pythonに関心のある公認会計士(CPA)の勉強会として発足しましたが、現在ではより広く、テクノロジー全般に興味を持ち、探求する意欲のある、会計士、経理財務人材、エンジニアなどがメンバーとなって活動しています。
PyCPAは毎月勉強会を開催しており、もくもく会やセミナー、参加型ワークショップを行っています。
現在のコミュニティメンバーはSlack登録者ベースで170名ほど、2019年5月現在の勉強会の累計参加者は250名を超えます。
PyCPAコミュニティと勉強会への参加は無料となっており、運営事務、会場確保、講師の登壇等はすべて、コミュニティのビジョンに共感していただいている組織・個人のボランティアでなりたっています。
PyCPAにコミュニティメンバーとして参加したい方はPyCPAのSlackにご登録ください。
ツイッターでのPyCPAコミュニティメンバーのやり取りは、こちらからご覧いただけます。
リアル・オプション輪読会の概要
今回の勉強会は初の輪読会となりました。
輪読会とは、複数人で同じ本を読み進め、集まって内容を共有し、理解を深める方法です。
今回の輪読会で取り組んだのは『モンテカルロ法によるリアル・オプション分析』という専門書です。
この本は、ファイナンス(金融工学)とプログラミング(ExcelVBA)を用いて、経営意思決定の柔軟性が創出する価値=リアル・オプションを定量的に評価する手法が学べる本です。
参考記事:『モンテカルロ法によるリアル・オプション分析』内容の概説、こんな人におすすめ、いい点と注意点
本書はリアル・オプションを学ぶとても良い題材である一方で、なかなか難易度の高い本だったので、輪読会の題材にしました。
今回は初回ということで、輪読会の目的や進め方について説明しました。
参考記事:【開催前夜】リアル・オプション輪読会の目的、理由、進め方
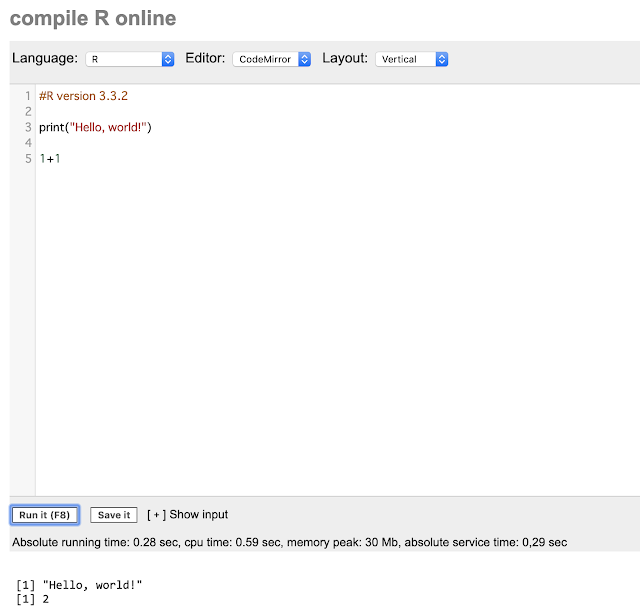
輪読は第1章を扱いました。
第1章はプログラミング言語ExcelVBAの基礎で、テキストに書かれたコードを入力しながら参加者全員で読み進めました。
VBAの始め方や、変数や関数の定義、for文やDoWhile文などの基本構文、配列の使いかたなどについて学びました。
途中、ファシリテーターから「このコードはモンテカルロ法のこんなシーンで役に立ちます」「この構文は株価シミュレーションの計算で使います」というような解説をはさみながら進めました。
感想とフィードバック
予習について
全員でコードを入力しながら、さくさくと読み進めたので、ちょっと駆け足気味になりました。
この点に関して、参加者から「次回は予習して来ようと思った」という声が上がりました。
事前に準備をしてくれば、輪読会をより意義深いものにできそうです。
バグについて
事前に予習してきた方も、その場でコードを入力した人も、みなさんバグ=プログラムが動かない問題に悩まされていました。
しかし、参加者のひとり(エンジニア)の方から「バグは出るもの、人は完璧じゃない、能率的にバグがとれればOK」という前向きな意見が出て、参加者の気持ちも楽になったように思います。
プログラミングにはバグがつきものですので、輪読会のように他の人と助け合える環境で学習を進めるのがよいと思います。
練習と実践について
プログラミングは一度勉強しても、使わなければすぐ忘れてしまう、という感想が出ました。
たしかに、人は忘れる生き物ですから、どんなに勉強しても使わなければ忘れてしまいます。
もし勉強したことを忘れたくないのであれば、お仕事で使うなり、勉強会で披露するなりして、知識の維持に努める必要がありそうです。
参加者アンケート結果報告
- 参加者の所属
- 参加理由
- 意見・感想・提案など
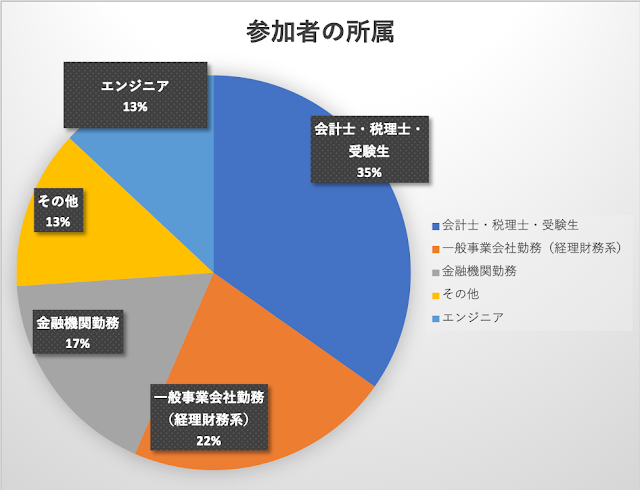
参加者の所属
次いで一般事業会社(経理財務系)の方、金融機関勤務と続きます。
輪読会の内容がプログラミングであったため、エンジニアの方の存在感はとても大きかったです。
会の最後にMVPを決めたのですが、AI開発がご専門のプログラマの方が絶大な支持を得て見事MVPを獲得されました。
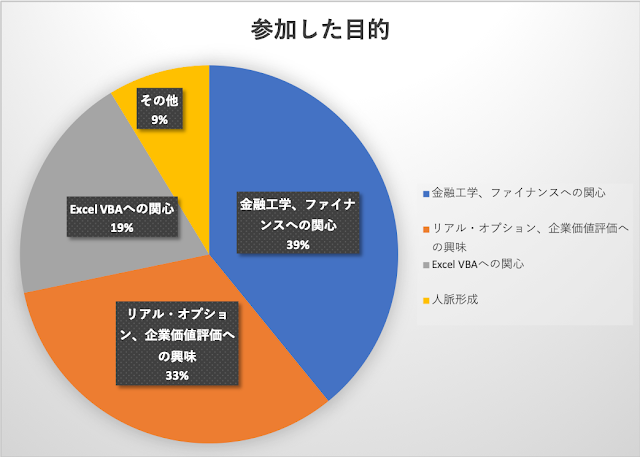
参加理由
みなさんお仕事で金融・ファイナンスに関わりがある方がほとんどで、その理解を深めたいという方が大多数でした。
リアル・オプションという経営意思決定のためのツールを学びたいという、このテキストの目的ど真ん中のかたもたくさんいらっしゃいました。
ファイナンスにせよ、VBAプログラミングにせよ、このテキストはとてもよい教材になりますので、是非チャレンジしてほしいと思います。
意見・感想・提案など
まったく門外漢ですが、なにか楽しそうだと思いました
モンテカルロ法という言葉ぐらいしか知らないので、その内容を理解したい
私も最初はそうでした。
モンテカルロ法という何やら凄い技術があるらしい、なんか楽しそう。
そういう興味が人生を豊かにしてくれると信じています。
一緒に楽しみましょう。
将来的に転換社債のプライシンクモデルを作りたいです!
業績連動型のストックオプション
モンテカルロ法は金融商品評価の強力なツールで、その応用範囲は膨大です。
輪読会での学びをきっかけに、よりアドバンストな内容に挑戦してみるのもいいでしょう。
意思決定にどう活かすのかに興味があります。
リアル・オプションは経営意思決定のツールとして有用です。
単に本を読み、ふーん、そういう手法があるのね、で終わらせることなく、是非輪読会で他の方とディスカッションすることで、ビジネスへの応用について探っていきましょう。
私もとても楽しみです。
まとめ
PyCPA リアル・オプション輪読会の振り返りについて述べました。
徐々にその裾野を広げつつ、コミュニティとしての輪郭を備え始めたPyCPAですが、まだまだ始まったばかりです。
みなさんの学ぶ意欲と発信で、一緒に楽しみましょう。












最近のコメント