こんにちは、毛糸です。
仮想通貨に再び注目が集まっています。
2017年に価格が高騰し、2018年に暴落した仮想通貨は、現代のバブルとして一躍有名になりました。
参考記事:ビットコインはバブルである
仮想通貨パッケージcryptoをインストールする方法
仮想通貨価格の時系列データ(ヒストリカルデータ)の入手方法
install.packages("crypto", dependencies = TRUE)
library(crypto)
#仮想通貨のリストを表示 crypto_list()
> #仮想通貨のリストを表示 > crypto_list() # A tibble: 2,212 x 6 symbol name slug rank exchange_url history_url <chr> <chr> <chr> <dbl> <chr> <chr> 1 BTC Bitcoin bitcoin 1 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 2 ETH Ethereum ethereum 2 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 3 XRP XRP ripple 3 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 4 BCH Bitcoin… bitcoin… 4 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 5 EOS EOS eos 5 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 6 LTC Litecoin litecoin 6 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 7 BNB Binance… binance… 7 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 8 BSV Bitcoin… bitcoin… 8 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 9 USDT Tether tether 9 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… 10 XLM Stellar stellar 10 https://coinmarketcap.com/… https://coinmarketcap.com/currencies/… # … with 2,202 more rows
ビットコイン(BTC)の価格データからリターンとリスクを計算する
ヒストリカルデータの取得
#crypto_history(coin = NULL, limit = NULL, start_date = NULL #end_date = NULL, coin_list = NULL, sleep = NULL) #仮想通貨の価格等情報を取得 #dateはyyyymmdd形式で。NULLとすると最長期間 BTC<-crypto_history(coin = "BTC", start_date = NULL,end_date = NULL)
BTC_saikin<-crypto_history(coin = "BTC", start_date = "20190501",end_date = "20190530")
#データの先頭 head(BTC,1) #データの最後尾 tail(BTC,1)
BTC$closeのように$マークのあとに取り出したい列のラベルを指定します。終値を時系列データとして抽出
#BTCの終値情報を時系列として取り出す。 #時系列情報の開始日をBTC$date[1]と指定 BTC_price<-ts(BTC$close,start=BTC$date[1])
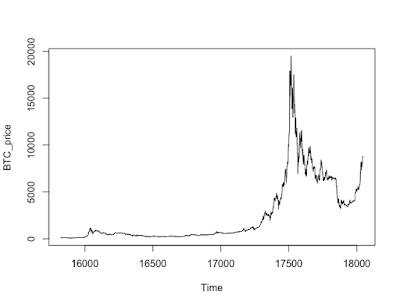
価格チャート
#type="l"は線グラフ plot(BTC_price,type="l")
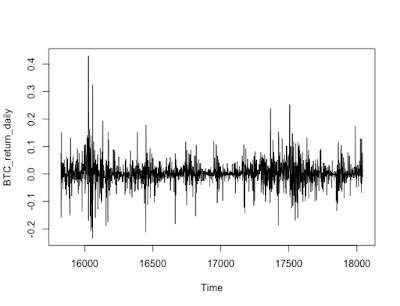
BTCの日次収益率(リターン)
#日次収益率 BTC_return_daily<-diff(BTC_price,lag=1)/lag(BTC_price,k=-1) plot(BTC_return_daily,type="l")
BTCリターンの平均と標準偏差(リスク)
mean(BTC_return_daily)*100 #[1] 0.2808807 #表示は% #年率換算では mean(BTC_return_daily)*100*365 #[1] 102.5215
標準偏差はsd()関数で計算できます。
sd(BTC_return_daily)*100 #[1] 4.333606 #表示は% sd(BTC_return_daily)*100*365^0.5 #[1] 82.79343









最近のコメント