こんにちは、毛糸です。
先日こんなつぶやきを見つけました。
この戦略が「けっこうな利回りになる」のは、偶然なのか、それとも市場原理に基づく収益機会なのか、
金融工学で大学院まで出てる毛糸は大変気になりましたので、少し掘り下げて考えてみます。
結論から言うと、レバETFのブルベアショートは必ず儲かる戦略ではありません。
この理由を、今回は数式で示します。
レバレッジETFとはなにか?(レバレッジとインバース、ブルとベア)
そもそもレバレッジETF(レバETF)とはなんでしょうか?
レバレッジETFとは、ある指数(TOPIXやS&Pなど)の日次騰落率の2倍の騰落率となるよう設計されたETFのことです。
日経225が今日2%上昇したとき、日経レバレッジETFは4%上昇する、というイメージです。
レバレッジETFの逆パターンもあります。
ある指数(TOPIXやS&Pなど)の日次騰落率の-2倍の騰落率となるよう設計されたETFがあり、これを(ダブル)インバースETFといいます。
日経225が今日2%上昇したとき、日経ダブルインバースETFは4%下落する(−4%上昇する)、というイメージです。
レバレッジETFをブル、インバースETFをベア、と呼ぶこともあります。
ブル(雄牛)は角を上へ突き上げるイメージから上昇を、ベア(熊)は爪を下へひっかくイメージから下落を象徴しています。
まとめです。
- レバレッジETFは、指数の日次変動の2倍の動きをする
- レバETFをブルとも言う
- インバースETFは、指数の日次変動の−2倍の値動きをする
- インバETFをベアとも言う
このレバ・インバETFには、日々の値動きが指数の3倍になるような商品も設計されています。
レバレッジETFのブルベアショート戦略とはなにか
では、最初に取り上げたツイートにもあった「レバETFのブルベアショート」とはどんな戦略なのでしょうか?
まず前提となるのが、「レバETFは減価する」という主張です。
レバレッジETFは長期で保有すると減価するため、長期投資に向かない、とされています。
こちらのサイトでも数値例を使って、長期投資に向かない理由を説明しています。
ここで、こんなことを思いつきます。
レバETF(ブル)とインバETF(ベア)を両方買うと、
日々の変動は完全に相殺される。
しかし、レバ・インバETFは減価するのだから、
このポートフォリオをショート(売建)することで、
リスクなしに収益が得られるのではないか?
こんな考えから生まれたのが「レバETFのブルベアショート」という戦略です。
本記事では、この戦略が「リスクなしに収益が得られる」ような取引ではないことを数式を使って説明します。
レバレッジETFはなぜ減価するのか
レバETFについて、
「日々の変動率の2倍動くのだから、長期で持っていても単純に指数の2倍になるだけでは?」
と思われる方もいるでしょう。
しかしこれは誤りです。
こちらのサイトでは「相加平均(算術平均)と相乗平均(幾何平均)」の考え方を使って、この考え方が誤りであることを説明しています。
本記事では「ETFの減価」とはどういうことか、より一般的に、数式で説明してみましょう。
レバETFが減価する(?)数学的理由
【0日目】
指数に1円を、2倍のレバETFにも同じく1円を投資することを考えます。
【1日目】
指数の変動率が\( r_1\)%だったとしましょう。
指数は変動し、\( 1+r_1\)円になります。
レバETFは変動率の2倍の値動きをするので、\( 1+2r_1\)円になります。
【2日目】
指数の変動率が\( r_2\)%だったとしましょう。
指数は変動し、\( (1+r_1)(1+r_2)=(1+r_1+r_2+r_1r_2)\)円になります。
\( 1+r_1+r_2\)円、ではありませんよ。
変動「率」は掛け算で増えていきます、複利効果というやつです。
\( r_1r_2\)の項が、複利効果を表しています。
レバETFは変動率の2倍の値動きをするので、\( (1+2r_1)(1+2r_2)=(1+2r_1+2r_2+4r_1r_2)\)円になります。
この式を少し変形して
\[ \begin{split}
1+2r_1+2r_2+4r_1r_2=1+2(r_1+r_2+r_1r_2)+2r_1r_2
\end{split} \]
と考えてみましょう。
\( (r_1+r_2+r_1r_2)\)は2日目までの指数の変動率ですから、
レバETFの変動率=\(1+2\)指数の変動率\(+2r_1r_2 \)
という関係にあります。
この式からわかることは、
2日間のレバETFの変動率は、2日間の指数の変動率と\( 2r_1r_2\)だけズレる
ということです。
さらに言えば、\( r_1\)と\( r_2\)の符号が逆の場合、\( 2r_1r_2\)の符号はマイナスになるので、
レバETFの変動率<\(1+2\)指数の変動率
となります。
\( r_1\)と\( r_2\)の符号が逆の場合、つまり上げと下げが交互に来た場合、レバETFの変動率は指数の変動率の2倍を下回ります。
これが減価の正体です。
一方、\( r_1\)と\( r_2\)の符号が同じ場合、つまり上げ・下げが繰り返した場合、
レバETFの変動率>\(1+2\)指数の変動率
となり、レバETFの変動率は指数の変動率の2倍を上回ります。
この数学的事実から言えるのは、
そもそもレバETFが減価していくというのは確定した話ではなく、
変動の方向が同じような値動きをしたときは減価せず、
文字通り収益にレバレッジがかけられる。
ということです。
「レバETFは減価する」と書いてある記事をよく見てみてください、変動率がプラスとマイナスを行き来しているような設定になっているはずです。
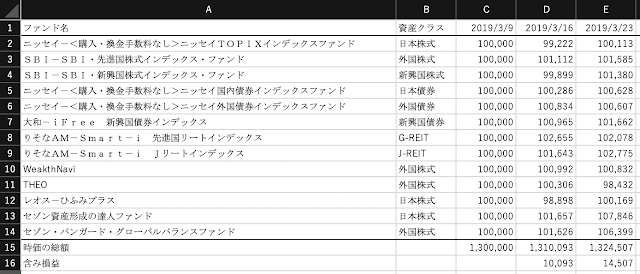
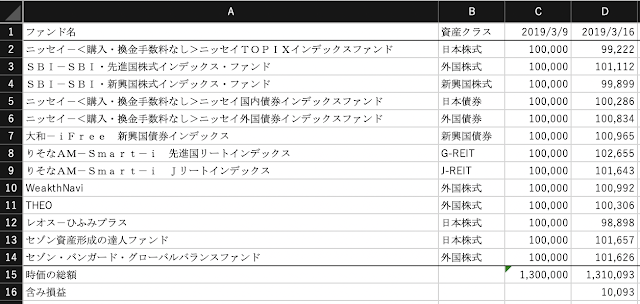
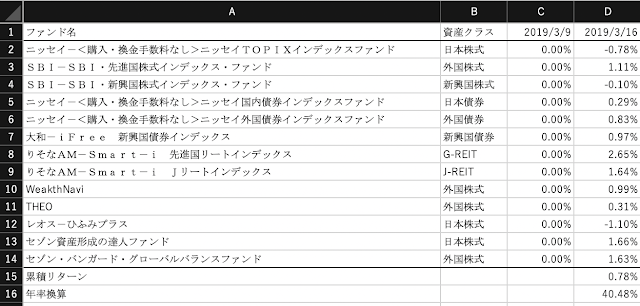
以下の表にまとめました。
- 2倍レバETFを複数日保有したときの累積収益率は、指数の累積収益率の2倍にはならない
- 両者の差はレバETFが生む複利効果を意味する
- 指数の上げと下げが交互に起こる場合、レバETFは減価する
- 指数の上げと下げが継続して起こる場合、レバETFは指数の2倍以上の収益を生む
レバレッジETFのブルベアショートが必ずしも儲からない理由
レバETFは必ずしも減価しない、ということが数理的にわかりました。
したがって、レバETFの減価が戦略の前提になっていたレバETFのブルベアショートも、必ずしも収益を生まないのではないか、と考えられます。
次はレバETFのブルベアショートが必ずしも収益を産まない理由を数式と図で考えてみます。
レバETFのブルベアショートが儲かる(?)数学的理由
【0日目】
指数2円をロングし、2倍のレバETFに1円、-2倍のインバETFを1円、それぞれショートする戦略することを考えます。【1日目】
指数の変動率が\( r_1\)%だったとしましょう。
指数は変動し、\( 2\times(1+r_1)=2+2r_1\)円になります。
レバETFは変動率の2倍の値動きをするので、\( 1+2r_1\)円のショート・ポジションになります。
インバETFは変動率の-2倍の値動きをするので、\( 1-2r_1\)円のショート・ポジションになります。
レバETFとインバETFのポートフォリオ(以下、ブルベアといいます)の価値は、\( 1+2r_1+1-2r_1=2\)円(ショート)です。
すでに指数とブルベアの価格差が\( 2r_1\)円出てきていますね。
\( r_1\)がプラスかマイナスかで、この戦略は利益にも損失にもなります。
【2日目】
指数の変動率が\( r_2\)%だったとしましょう。
指数は変動し、\( 2\times(1+r_1)(1+r_2)=2+2r_1+2r_2+2r_1r_2\)円になります。
レバETFは変動率の2倍の値動きをするので、\( (1+2r_1)(1+2r_2)=1+2r_1+2r_2+4r_1r_2\)円(ショート)になります。
インバETFは変動率の-2倍の値動きをするので、\( (1-2r_1)(1-2r_2)=1-2r_1-2r_2+4r_1r_2\)円(ショート)になります。
レバETFとインバETFのポートフォリオ(以下、ブルベアといいます)の価値は、\( 2+8r_1r_2\)円(ショート)です。
したがって、2日目における指数とブルベアの価格差は\( 2r_1+2r_2-6r_1r_2\)円となります。
この式からわかることは、
- 2日間のブルベアの変動率は、2日間の指数の変動率とずれ、そのズレが損益となる
- 損益の方向(利益か損失か)は\( r_1\)と\( r_2\)の符号、つまり日次の指数変動率の方向による
ということです。
たとえば1日目の変動が1%、2日目の変動が1%であった場合には、ブルベアショート戦略から利益が得られますが、
1日目の変動が-1%、2日目の変動が-1%であった場合には、ブルベアショート戦略からは損失が生じます。
具体的に\( r_1\)と\( r_2\)がどういうときに利益になり損失になるのか、というと、
- \( r_1>0\)かつ\( r_2>0\)、つまり上昇が続けば利益
- \( r_1<0\)かつ\( r_2<0\)、つまり下落が続けば損失
- それ以外の場合、変動率の大小関係による
となります。
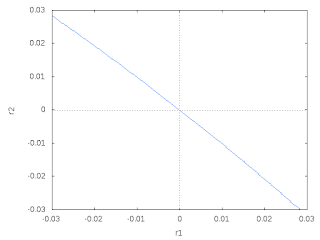
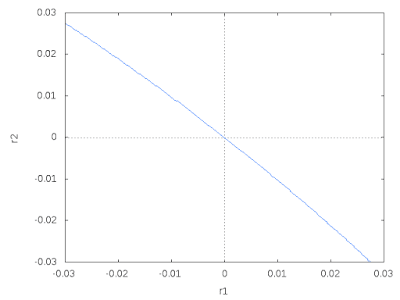
それを表しているのが以下の図です。
横軸が1日目の指数変動率\( r_1\)、横軸が2日目の指数変動率\( r_2\)で、グラフの上側がブルベアショートで利益を獲得できるゾーン、下側が損失ゾーンです。
以上のことから、レバETFのブルベアショートは、必ずしも収益を生む戦略ではなく、指数の変動の方向によっては損失を被る可能性もある、ということがわかります。
まとめ
本記事では、レバレッジETFが減価すると言われている理由を数式で明らかにし、「レバETFのブルベアショート」という戦略が必ずしも収益を生まないことを数式とグラフで示しました。
市場で広く知られている商品の組み合わせから、安定的な高収益を生み出すことは難しいものです。
うまい話のように思えたら、きちんと検証してみる姿勢が、投資においては重要だと考えます。
分析が得意な方の中には、過去のデータ(バックテスト)からこの戦略の有効性を実証している方もいるかも知れません。
いずれ、実際のデータやモンテカルロ・シミュレーションを用いて、レバETFのブルベアショート戦略の有効性を検証する機会を儲けようと思います。
参考文献
本記事を書くに当たり、以下の本が大変参考になりました。
神谷政敏『運もお金もない人のための資産の増やし方』
数式を計算するに際しては、数式処理ソフトMaximaを利用しました。
複雑な数式の計算を自動でやってくれるので、大変便利なツールです。
梅野 善雄 『いつでも・どこでも・スマホで数学! Maxima on Android活用マニュアル』
リンク




























最近のコメント