1. ホーム /
  2. 2019年 8月

2019年 8月 の投稿一覧

連続時間モデルにおけるクリーン・サープラス関係（Clean surplus relation, CSR）

こんにちは、毛糸です。

先日、以下の記事で、会計数値（純資産や営業資産）の変動を規定する関係式について述べました。

【参考記事】
会計数値の時系列構造を決める関係式｜クリーン・サープラス関係、金融資産関係、営業資産関係

上記記事に示したクリーン・サープラス関係（Clean Surplus Relation, CSR）とは、企業の純資産の変動を示す以下の関係式のことです。
\begin{equation} \begin{split}
bv_t=bv_{t-1}+ni_t-d_t
\end{split} \end{equation}

ここで\( bv_t\)は時点\( t\)における純資産の金額、\( ni_t\)は純利益、\( d_t\)は配当を示しています。クリーン・サープラス関係は、純資産\( bv_t\)を離散的な時間単位で観測した、差分方程式を表しているといえます。

ということは、これを連続時間で考える、つまり純資産の微分方程式を考えるのは、極めて自然な流れではないでしょうか。

素朴に考えると、１期間で成り立つクリーン・サープラス関係を、時間区間\( \Delta t\)でも成り立つと考え

\begin{equation} \begin{split}
bv(t+\Delta t)-bv(t)=ni(t)\Delta t-d(t)\Delta t
\end{split} \end{equation}

と表し、時間区間\( \Delta t\)を\( 0\)に近づけた極限を考えると
\begin{equation} \begin{split}
dbv(t)=ni(t)dt-d(t)dt
\end{split} \end{equation}
のように表せてもよさそうなものです。

これは純資産\(bv \)の微分方程式になっています。

当然ながらこれを積分すると

\begin{equation} \begin{split}
bv(t)=bv(0)+\int_0^t ni(s)ds-\int_0^t d(s)ds
\end{split} \end{equation}
となり、
「ある時点の純資産は、当初純資産に、利益の累積額を足して、配当として流出した分を控除した額として決まる」
という当たり前の結果が成り立ちます。

会計では通常、会計数値は連続的には観測されず、四半期ごととか１年ごとといった離散時間でのみ観測されます。

しかしながら、理論上は瞬間瞬間に決算をし会計数値を確定させるような手続きを踏めば、もしくはその時点で決算を行えば観測されたであろう「仮想の」会計数値を考えれば、連続時間でクリーン・サープラス関係が成り立つと考えても問題はなさそうです。

むしろクリーン・サープラス関係を微分方程式として表すことができれば、解析学のツールを活用することが出来、分析の幅が広がることも期待されます。

会計学の論文では実際に、この連続時間版クリーン・サープラス関係を扱っているものがいくつかあります。

時間をとってこれらの論文を読み込んでみたいと思います。

RESIDUAL INCOME, REVERSIBILITY AND THE VALUATION OF EQUITY(PDF)
Mark Tippett and Fatih Yilmaz
LINEAR INFORMATION DYNAMICS, AGGREGATION, DIVIDENDS AND “DIRTY SURPLUS” ACCOUNTING(PDF)
David Ashton, Terry Cooke, Mark Tippett and Pengguo Wang
A valuation model for firms with stochastic earnings（PDF）
Steven Li

「安全資産」という言葉の誤用について

こんにちは、毛糸です。

先日こんなツイートをしました。

本記事では「安全資産」という言葉の正しい意味を説明し、誤用例のどこが誤っているのかを解説します。

安全資産の定義

安全資産（risk free asset）は経済学やファイナンスの専門用語です。

安全資産とは、投資時点において収益（額・率）が確定している資産です。

株式などのリスクある資産は、投資時点において（資産の購入時点において）、将来いくら返ってくるかが明らかではありません。

100万円で買った株が120万円になることもあれば、80万円になってしまうこともあり、収益が確定していません。

収益が確定していない、つまり不確実であることを、「リスクがある」「リスキーだ」といいます。

安全資産とは、収益の不確実性がない資産のことであり、無リスク資産ともいいます。

金や円は安全資産？いいえ、誤用です

安全資産とはあらかじめリターンがわかっている資産ですから、以下のようなものは安全資産ではありません。

  1. 相場全体が下落しているときにこそ値上がりする資産
  2. 下落相場で買われやすい退避先資産
  3. 投資収益率のボラティリティが低い資産

相場全体が下落しているときにこそ値上がりする資産

株式相場全体がマイナスムードの時にも株価が下がりづらかったり、むしろ値上がりするような資産を、安全資産と称する場合がありますが、誤用です。

相場全体の動きと、個別の資産の動きの連動性は、ベータと呼ばれます。

相場全体が下がっても、価格が上がるような資産は、負のベータを持つ資産といえますが、この場合も投資時点でリターンが確定しているわけではないので、安全資産ではありません。

下落相場で買われやすい退避先資産

金（ゴールド）や円を安全資産と称する場合がありますが、誤用です。

一般用語としてなんとなく「安全」であるというニュアンスは伝わりますが、当然ながらこれらは投資時点でリターンが決まっていないので、安全資産ではありません。

投資収益率のボラティリティが低い資産

収益の変動性、つまり期待収益から上下にどれだけ変動しうるかの尺度を、ボラティリティといいます。

ボラティリティが高いということは、それだけ収益の振れ幅が大きい資産ということであり、ハイリスクです。

収益のボラティリティが小さい資産はローリスクであり、これを安全資産と称する場合がありますが、誤用です。

例えば、インフラ系企業（電気やガス）の株は従来、景気変動の影響を受けづらい銘柄をディフェンシブ銘柄として認知されていました。

しかし、某電力会社がああいうことになったこともわかるように、ボラティリティが低くとも、価格変動のリスクから完全に切り離されているわけではないので、安全資産ではありません。

安全資産は実際に存在するのか

デフォルト（貸倒れ）のない債券が唯一、安全資産です。

貸出時にリターンが決まっており、必ず返済されるので、これは定義通り、安全資産になります。

ただし、物価変動を考慮すると結論は変わります。

物価変動を考慮した場合の安全資産は、国家などのデフォルト懸念のない主体が発行する物価連動債です。

名目上の利回りが投資時点で既知の名目債は、物価変動により実質価値が上下するので、安全資産ではありません。

現在、一般市民が投資可能な物価連動国債は発行されていないですし、国家であってもデフォルト懸念がないとは言えないので、真の意味での安全資産はありません。

YouTubeで量子力学が勉強できる時代

こんにちは、毛糸です。

数学をライフワークとしている私ですが、この世界のルール・理（ことわり）を数理的に解き明かす物理学にも当然興味を持っています。

物理学には物理学特有の数式表現が数多く存在しています。

ブラケット記法とか、アインシュタインの縮約記法とか、物理を論じる上で都合のいい数式の記述方法には色々あります。

私は物理学をきちんと勉強したことがなかったので、それらに出くわすときはしばらく時間をとって調べる必要があります。

今日も調べ物をしていましたら、偶然こんな動画を見つけました。

予備校のノリで学ぶ「大学の数学・物理」というチャンネルでは、大学レベルの数学と物理学を、「予備校のノリで学ぶ」ことができます。

講師のたくみ先生の講義は大変わかりやすく、教育系YouTuberとして有名なようです。

これまでは、なにか勉強をしたいと思ったら、その分野の教科書を読み、学校に通い、もしくは近くの詳しい人に聞いたり、ネットの文字情報を読み込む必要がありました。

しかし、インターネット環境が整う中で、このような動画による教材が多く提供されつつあり、学びの幅は更に広がっています。

また、SNSの発展により、同じ興味を持つ人と、物理的な距離を問わずつながることができるようになりましたし、オンラインの人間関係を発展させ気軽にリアルな勉強会を開くこともできるようになっています。

そう、現代は学びを楽しむ人にとっては、とても幸福な時代なのです。

私も自分の興味を共有したくて、勉強会を開いたりしていますが、普段の仕事だけでは得られないつながりを持つことができ、とても楽しいです。

【参考記事】
勉強会「意識高い……」「レベル高そう……」いやいや、誤解してませんか？

 

学ぶことを苦痛と思わず、知ることを純粋に楽しめるようになったら、現代社会の充実感を噛みしめることができるでしょう。

今回紹介した動画は量子力学（量子論）の解説ですが、量子論を考えるには「波」に関する理解が必須です。

波（波動）は高校物理でも扱いますので、高校レベルの参考書を読んでみることから始めるのが良いでしょう。

私も以下の本が高評価だったので、この夏の宿題として、読んでみようと思っています。



会計数値の時系列構造を決める関係式｜クリーン・サープラス関係、金融資産関係、営業資産関係

こんにちは、毛糸です。

こんな本を読んでいます。

この本は、企業が発行する株式を評価する手法を、会計学と経済学の立場から論じる研究書です。

この中に、会計学における重要な方程式が取り上げられていたので、メモしておきます。

クリーン・サープラス関係（Clean Surplus Relation, CSR）

クリーン・サープラス関係（Clean Surplus Relation, CSR）とは、企業の純資産の変動を示す以下の関係式のことです。

\begin{equation} \begin{split}
bv_t=bv_{t-1}+ni_t-d_t
\end{split} \end{equation}

ここで\( bv_t\)は時点\( t\)における純資産の金額、\( ni_t\)は純利益、\( d_t\)は配当を示しています。

つまり、ある時点の純資産額は、一期前の純資産額に、その期の利益を加え、株主に支払った額を差し引いた金額として定まる、ということです。

純資産額\( bv_t\)は、金融（純）資産\( fa_t\)と営業（純）資産\( oa_t\)に分けられると仮定します。

\begin{equation} \begin{split}
bv_t=fa_t+oa_t
\end{split} \end{equation}

純利益\( ni_t\)は、金融（純）利益\( fi_t\)と営業（純）利益\( oi_t\)に分けられると仮定します。

\begin{equation} \begin{split}
ni_t=fi_t+oi_t
\end{split} \end{equation}

金融資産関係（Financial Asset Relation, FAR）

金融資産関係（Financial Asset Relation, FAR）とは、金融（純）資産の変動を示す以下の関係式のことです。

\begin{equation} \begin{split}
fa_t=fa_{t-1}+fi_t+fcf_t-d_t
\end{split} \end{equation}

ここで\( fcf_t\)は時点\( t\)におけるフリーキャッシュフローです。

金融資産関係が成り立つためには、株主への配当は金融（純）資産を通じて行われるという前提を置く必要があります。

この前提のもとで、ある時点の金融（純）資産額は、一期前の金融（純）資産額に、その期の金融（純）利益とフリーキャッシュフローを加え、株主に支払った額を差し引いた金額として定まります。

営業資産関係（Operating Asset Relation, OAR）

営業資産関係（Operating Asset Relation, OAR）とは、営業（純）資産の変動を示す以下の関係式のことです。

\begin{equation} \begin{split}
oa_t=oa_{t-1}+oi_t-fcf_t
\end{split} \end{equation}

営業資産関係（OAR）は、クリーン・サープラス関係（CSR）と金融資産関係（FAR）が成り立つときには当然成り立ちます。

ある時点の営業（純）資産額は、一期前の営業（純）資産額に、その期の営業（純）利益を加え、フリーキャッシュフローを差し引いた金額として定まります。

会計ベースの資産価格理論

CAR、FAR、OARは、ファイナンスの基本原則「無裁定の原則」と組み合わせると、会計数値をベースとした資産価格理論につながっていきます。
ファイナンスでは、ある資産が生み出す配当や利息の割引現在価値が、その資産の価格に等しいという関係式を考察しますが、これは基本的にはキャッシュフローの世界の考え方です。
しかし、上記のような会計関係（Accounting Relation(s)）を組み合わせることで、キャッシュフローの世界から、会計数値の世界へと、資産価格の理論を発展させることができます。
もし興味があれば、財務諸表分析などを扱うテキストに説明があるので、読んでみると良いでしょう。

算術リターンと幾何リターンの違いについて

こんにちは、毛糸です。

本記事では、投資リターンの2つの概念、算術リターンと幾何リターンの違いについてまとめます。

記事中では、時点( t)における資産（株など）の価格を( S_t)と表し、算術リターンと幾何リターンの計算式の違いを説明します。

算術リターンとは

算術リターン（Arithmetric return）は、いわゆるリターン（収益率）として通常イメージするものです。

時点( t)で明らかになる算術リターン( r_t^A)は、次のように計算されます。
begin{equation} begin{split}
r_t^A=frac{ S_{t}-S_{t-1}}{S_{t-1} }=frac{ S_{t}}{S_{t-1} }-1
end{split} end{equation}

すなわり、算術リターンとは、投資額( S_{t-1} )に対する、投資額の増分( S_{t}-S_{t-1})の割合のことです。

この式を変形して得られる
begin{equation} begin{split}
R_tequiv 1+r_t^A=frac{ S_{t}}{S_{t-1} }
end{split} end{equation}は、投資が何倍になったかを示しており、( R_t)を粗収益率（グロスリターン）と呼びます。( r_t^A)は純収益率（ネットリターン）といいます。

幾何リターンとは

時点( t-1)の株価( S_{t-1})は、次の日には( S_t)に変化します。したがって、ある粗収益率( R)を用いて
begin{equation} begin{split}
S_t=S_{t-1}R_t
end{split} end{equation}と表わせます。

資産価格は負にはなりませんので、( R_t)は常に0以上の値を取ります。

ところで、自然対数の底（ネピア数）( e(=2.718cdots))は何乗しても0以上の値になることがわかっていますから、( R_t=e^x)と書いても間違いではありません。

つまり
begin{equation} begin{split}
S_t=S_{t-1}e^x
end{split} end{equation}が成り立ちます。

この( x)を決めてやれば、株価は( S_{t-1})から( S_t)に変化することがわかりますから、( x)はある意味で収益率を表しているといっても良いわけです。

この( x)をあらためて( r_t^G)と表して、
begin{equation} begin{split}
S_t=S_{t-1}e^{r_t^G}
end{split} end{equation}という関係式が成り立つとき、( r_t^G)を幾何リターン（Geometric return）といいます。

この式を変形すると
begin{equation} begin{split}
e^{r_t^G}&=frac{ S_t}{ S_{t-1}}\
Leftrightarrow r_t^G&=logleft( frac{ S_t}{ S_{t-1}}
right)end{split} end{equation}となり、対数が現れます。

幾何リターンは別名、対数リターンと呼ばれますが、それは幾何リターンが価格比( frac{ S_t}{ S_{t-1}})の対数として計算されることに由来しています。

算術リターンと幾何リターンの関係

算術リターンと幾何リターンは、いずれもリターン（収益率）を表す指標ですが、一見するとその計算方法はまるで異なっています。
しかし、実は両者には密接な関係があるのです。
数学的な話を後回しにして結論を述べると、リターンがあまり大きくないときには、
begin{equation} begin{split}
r_t^Afallingdotseq r_t^G
end{split} end{equation}つまり算術リターンと幾何リターンはほぼ同じ値になります。

証明

幾何リターンと算術リターンの定義から、
begin{equation} begin{split}
r_t^G&=logleft( frac{ S_t}{ S_{t-1}}right)\
&=logleft( 1+frac{ S_t-S_{t-1}}{ S_{t-1}}right)\
&=logleft( 1+r_t^Aright)\  end{split} end{equation}が成り立ちます。

対数関数( log(1+x))は( x)が小さいとき、( x)に近似することが知られているので、
begin{equation} begin{split}
logleft( 1+r_t^Aright)fallingdotseq r_t^A
end{split} end{equation}となり、( r_t^Afallingdotseq r_t^G )がわかります。

対数関数( log(1+x))が( x)に近似することは、対数関数をマクローリン展開することでわかります。

算術リターンと幾何リターンの性質の違い

算術リターンと幾何リターンは、リターンが小さければほぼ同じ値を取りますが、リターンが大きければその差は無視できないものになります。
たとえば暗号資産のリターンは、一日で倍増したり半減したりしますから、算術リターンと幾何リターンの違いは大きくなります。
また、投資額が0になるような最悪のケースでは、算術リターンは

begin{equation} begin{split}
r_t^A=frac{ 0-S_{t-1}}{S_{t-1} } =-100%
end{split} end{equation}と計算されるのに対して、幾何リターンは
begin{equation} begin{split}
r_t^G=logfrac{ 0}{ S_{t-1}}=-infty
end{split} end{equation}と計算され、かなり差が出ます。

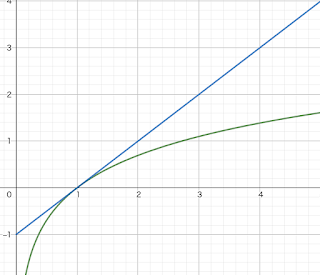
以下の図は青線で算術リターンを、緑線で幾何リターンを、それぞれ表していますが、常に算術リターンのほうが大きな値を取ることがわかります。
投資成績がふるわないときは、算術リターンを使うことでマイナス幅を小さめに表現することができます。
公表されるリターンが算術リターンなのか幾何リターンなのかは、十分注意する必要があります。

節税効果を企業価値に織り込む2つの方法

こんにちは、毛糸です。

最近こんな本を読んでいます。

本書『Equity Valuation』は、企業が発行する株式の評価方法について、会計学と経済学の立場から論じた研究書です。

この本の中で、節税効果（タックスシールド）を企業価値に織り込む2つの方法について述べられていたので、簡単にまとめておきます。

税引き後資本コスト（WACC）による方法

1つ目の方法が、フリーキャッシュフローや営業利益などの会計数値を割り引く際に用いる資本コストとして、税引き後の割引率を用いる方法です。

フリーキャッシュフローは債権者と株主に配分されるべきキャッシュフローで、これを以下のように定義される税引き後WACC（加重平均資本コスト）で割り引くことで、企業価値を算出できます。

\begin{equation} \begin{split}
k=\frac{ E}{ D+E}k_E+\frac{ D}{ D+E}(1-\tau)k_D
\end{split} \end{equation}

ここで\( E\)は株主資本、\( D\)は負債、\(k_E \)は株主資本コスト、\( k_D\)は負債コスト、\( \tau\)は税率です。

この方法はPenman2007やLundholm&Sloan2004に詳しく説明してあるようです。

修正賞味現在価値法（Adjusted NPV、APV）

節税効果を企業価値に織り込むもうひとつの方法が、修正賞味現在価値法（Adjusted Net Present Value Method, APV）です。

この方法は、節税効果（タックスシールド）を営業活動から生じるキャッシュフローの一部であるかのように扱い、割引率には税引前のWACCを使って企業価値を計算をする方法です。

Grinblatt&Titman2002にはAPVによる企業価値評価が説明されているようです。

税引き後WACCとAPVの比較

いずれの方法でも、条件が同じであれば同一の結果を導きます。

しかし、『Equity Valuation』によれば、APV法のほうがより柔軟で、企業価値の源泉となる営業活動と（税引前で）NPVがゼロの金融活動とを区別する考え方と整合しているといいます。

倒産コストを明示的に扱うような応用的なケースにおいては、税引き後WACCによる計算では企業価値に「歪み」が生じます。

しかしAPV法によれば、倒産コストも営業活動の一部として、通常の割引計算のなかで対応できるため、適用範囲が広いのです。

税引き後WACCもAPVも、企業活動をいくぶん単純化しているため、必ずしも現実の問題を正しく捉えられない場面もありますが、企業価値評価の実務においては広く用いられる方法です。

日本語のコーポレート・ファイナンスの定番テキストにも、これらの方法が説明されているので、興味のある方は調べてみると良いでしょう。

【参考記事】
【ファイナンス・金融工学】おすすめテキストと有名大学の指定教科書・参考書まとめ

【君の知らない複式簿記4】簿記代数の教科書『Algebraic Models For Accounting Systems』とバランスベクトル

こんにちは、毛糸です。

【君の知らない複式簿記】シリーズ第4弾となる本記事では、複式簿記の代数的構造に関する研究書『Algebraic Models For Accounting Systems』についてお話します。

【君の知らない複式簿記】シリーズの過去記事は以下のリンクから辿ることが出来ます。

本記事は下記記事を読まれていない方にも理解いただける内容です。

【君の知らない複式簿記1】行列簿記の意義、性質、限界

【君の知らない複式簿記2】複式簿記の拡張、三式簿記

【君の知らない複式簿記3】複式簿記の代数的構造「群」

続きを読む

【投信定点観測】21週目｜インデックス、ロボアドバイザー、アクティブファンドに積立投資

こんにちは、毛糸です。

【投信定点観測】2019年8月第1週（スタートから21週目）の損益の報告です。

今週末における損益率は2.57%（年率4.56％）です。

損益状況

商品ごとの含み損益率は以下のようになりました。【投信定点観測】開始から21週間経過時の含み損益率は2.57%（年率換算で4.56％）で、先週から0.80%のプラスです。

インデックス投資信託の変動

決算シーズンを受けて買い戻しが広がり、日本株式は週間0.47%上昇、先進国株式は1.16%の上昇となりました。

ロボアドバイザーの振り返り

ロボアドバイザーのWealthNavi（ウェルスナビ）は今週+1.47%(含み損益2.87%)、THEO（テオ）は今週1.09%(含み損益1.37%)でした。

今週の含み損益ランキングは、【投信定点観測】の全14の投資先のうち、WealthNaviは第6位、THEOは第11位です。

▼ロボアドバイザーTHEO（テオ）は登録はこちらから！
THEO

▼ロボアドバイザーWealthNavi（ウェルスナビ）の登録はこちらから！

WEALTHNAVI（ウェルスナビ）

アクティブファンドの変動

日本株式に投資するアクティブファンドひふみ投信は、インデックスであるTOPIXの週間上昇率0.47%に対して、1.87%の上昇となり、優位なパフォーマンスを上げています。

まとめ

【投信定点観測】を始めて20週、累積リターンを見るとJ-REITの+9.11%から、日本株式（TOPIX)の-1.18%まで、資産クラスによって明暗が別れています。

日本株式については、アベノミクスで脅威的な上昇を見せたとはいえ、バブル崩壊と失われた20年のイメージが強く残っているためか、投資対象として魅力的に映らない人が多いようです。

しかし、市場の効率性を考えると、日本株式の先行きは現在の株価に反映されていると考えられるので、安易な思考で投資対象から除くのは懸命ではないように思います。

【参考記事】
「日本株に投資すると長期的には損」は本当か？

将来のリターンを予測するのは大変困難なことなので、個人投資家は広く分散した投資によって、リスクを低減するのが王道でしょう。

引き続き、投資信託による「コツコツ」積立投資で、安定的な資産形成を目指していきます。

クリーン・サープラス関係と最適配当戦略

こんにちは、毛糸です。

最近、企業の配当はどう決まるか？ということを考えています。

配当とは、企業が獲得した利益を株主に分配することであり、株主にとってみれば投資の回収を意味します。

配当は、会計的には純資産の一部を取り崩すと同時に現預金を社外に流出させるものです。

配当と純資産などの会計数値の関係は、以下の「クリーン・サープラス関係」と呼ばれる関係式で記述されます。

\begin{equation}\begin{split}
B_t=B_{t-1}+e_t-d_t
\end{split}\end{equation}

この式は、時点\(t\)における純資産の額\(B_t\)は、1期前の純資産額\(B_{t-1}\)に\(t\)期の利益\(e_t\)を加え、配当\(d_t\)を差し引いた額として決まる、という規則を示しています。

配当\(d_t\)はキャッシュフローであるのに対し、純資産額\(B_t\)や利益\(e_t\)は会計数値ですから、キャッシュフローを中心とした理論展開が行われるファイナンスと会計とは、このクリーン・サープラス関係を通じて関連付けられることになります。

ファイナンスでは配当の割引現在価値として株価が決まるという「配当割引モデル」がよく知られていますが、これをクリーン・サープラス関係と組み合わせることで、会計数値に立脚した「残余利益モデル」と呼ばれる会計数値ベースの株式評価モデルが構築できます。

配当割引にせよ残余利益モデルにせよ、配当はそれ自体が確率変数であると考えて理論展開されることが多いです。

しかしながら、配当は企業が株主との関係を伺いながら、ある意味で「適切な」水準で「決定」するものです。

したがって、その決定プロセスを考察することなしに、天下り的に確率変数（ランダムな変数）と考えてしまうのはよくないのではないかと考えています。

私はこの問題意識に基づき、企業はどんな意思決定に基づき「最適な配当戦略」を決めているのかを、経済学的観点から検証しています。

何か発見があったら、ブログでも取り上げたいと思います。

Warning: Trying to access array offset on value of type bool in /home/r1406503/public_html/keito.luxe/wp-content/themes/xeory_base/lib/functions/bzb-functions.php on line 299

Warning: Trying to access array offset on value of type bool in /home/r1406503/public_html/keito.luxe/wp-content/themes/xeory_base/lib/functions/bzb-functions.php on line 301
class="col-md-4" role="complementary" itemscope="itemscope" itemtype="http://schema.org/WPSideBar">