こんにちは、毛糸です。
【投信定点観測】2019年5月第4週(スタートから11週目)の損益の報告です。
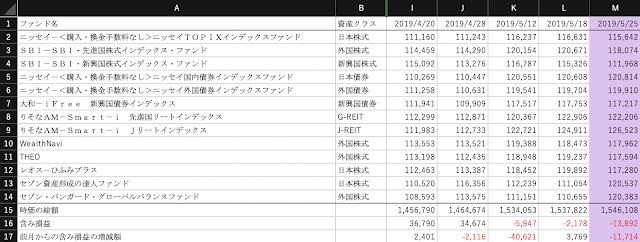
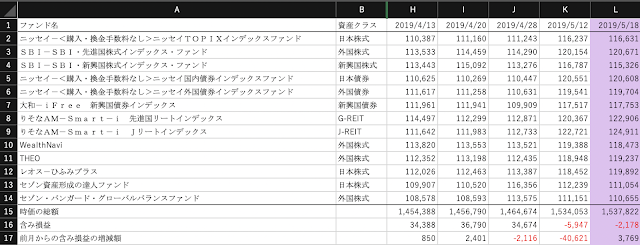
今週末における投資総額は156万円、含み損益は-13,892円、損益率は-0.89%(年率-2.89%)です。
損益状況
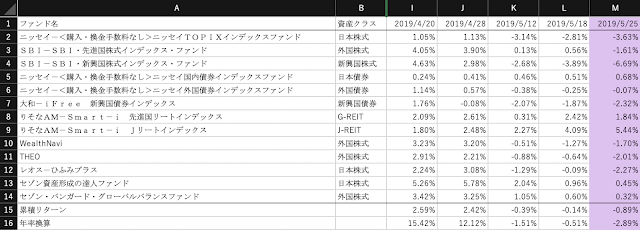
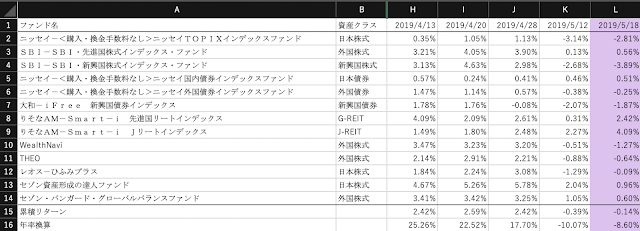
損益率に直すとこんな感じです。今週末の損益率は-0.89%(年率換算で-2.89%)です。
年率換算の損益率の計算式が誤っていたので、今回修正しました。
インデックス投資信託の振り返り:株式総崩れとREIT続伸
中国通信機器メーカーファーウェイが米国市場から閉め出されるというニュースが報じられ、同社と取引のある企業の株価が下落。その不安感が相場全体に広がり暗雲が立ち込めています。
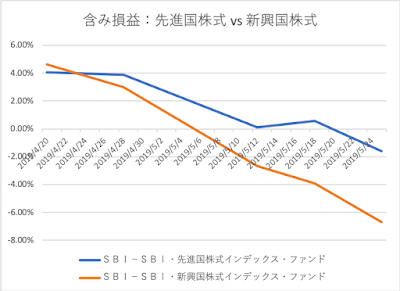
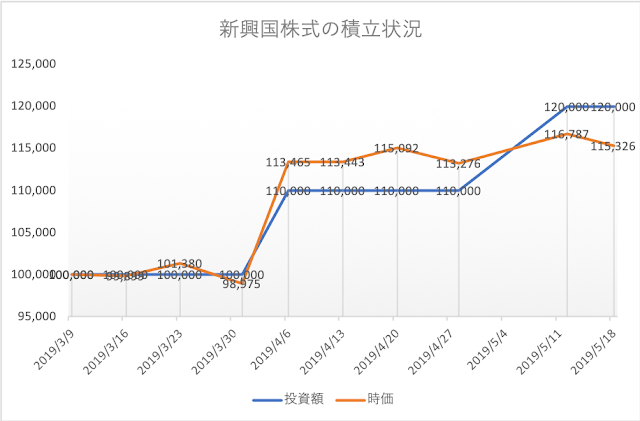
先進国株式は今週-2.16%の下落、中国を含む新興国株式も-2.80%の下落と大きなダメージです。
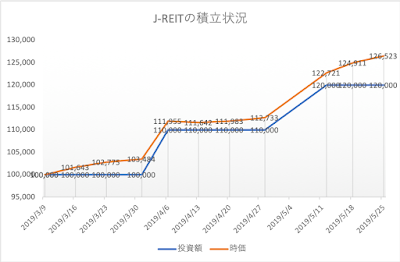
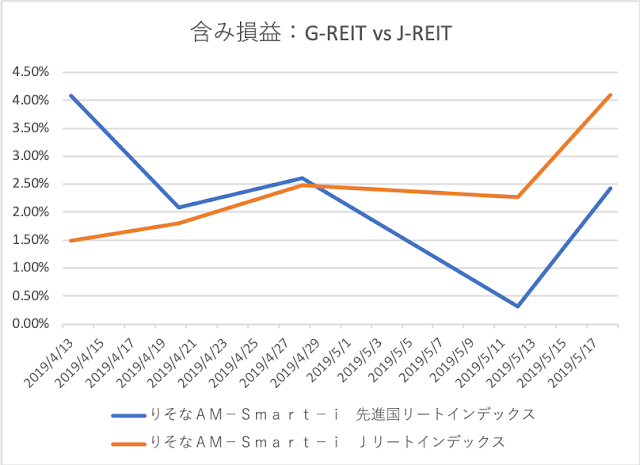
他方、J-REITは更に上昇し、週間+1.34%の伸びです。都市圏のオフィス需要が高水準で推移し、世界的な金利低下の流れが追い風となり、資金流入が続いているようです。
市場全体が下げているときは、裏を返せば安く資産を購入できるチャンスでもあります。
好景気になってから投資するのでは遅いので、是非このタイミングでインデックス投信の積立投資を初めてみてください。
(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”お金は寝かせて増やしなさい”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51xHIGALUZL.jpg”,”/51UFsW4HuvL.jpg”,”/51d7m7hcbYL.jpg”,”/61ULYpbutcL.jpg”,”/51uCgEZrhmL.jpg”,”/51ne7%2Bl4ysL.jpg”,”/51TjKtJWpzL.jpg”,”/51Zj-OmTSML.jpg”,”/410JAnn80uL.jpg”,”/51cjtS6tWPL.jpg”,”/61Q0Zvqja7L.jpg”,”/613B004TKQL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%8A%E9%87%91%E3%81%AF%E5%AF%9D%E3%81%8B%E3%81%9B%E3%81%A6%E5%A2%97%E3%82%84%E3%81%97%E3%81%AA%E3%81%95%E3%81%84-%E6%B0%B4%E7%80%AC%E3%82%B1%E3%83%B3%E3%82%A4%E3%83%81/dp/4894517833″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″}});
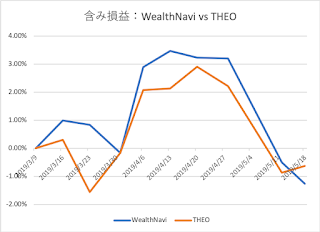
ロボアドバイザーの振り返り:THEO(テオ)とWealthNavi(ウェルスナビ)のリスク
【投信定点観測】を開始して11週目ということで、両者のリスク(リターンの標準偏差)を算出してみたところ、
- WealthNaviのリスクは1.70%/週
- THEOのリスクは1.59%/週
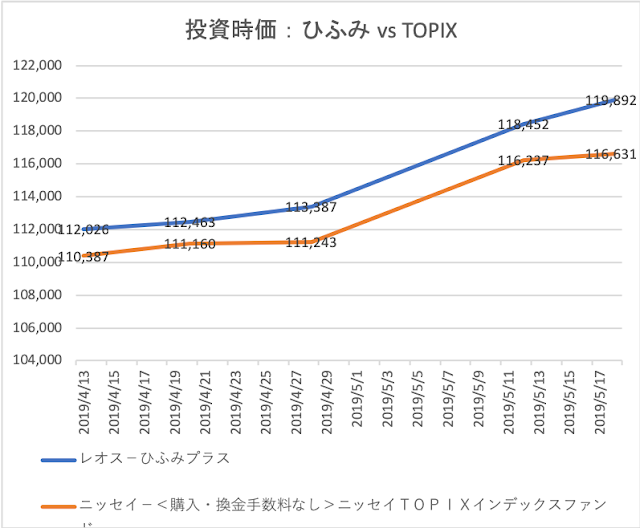
アクティブファンドの振り返り:ひふみとセゾン、明暗分かれる
現状、両者の明暗ははっきりしており、セゾン投信のパフォーマンスの高さが圧倒的です。
両者のリスク(リターンの標準偏差)を算出してみたところ、
- セゾン資産形成の達人のリスクは2.10%/週
- ひふみのリスクは1.90%/週
アクティブファンドはインデックスを上回る超過収益を得ることを目的としており、今の所、その目標は達成できていますので、今後の運用結果がたのしみです。
(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”いま選ぶべきアクティブ投信この8本!”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/51yqlV5edSL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%84%E3%81%BE%E9%81%B8%E3%81%B6%E3%81%B9%E3%81%8D%E3%82%A2%E3%82%AF%E3%83%86%E3%82%A3%E3%83%96%E6%8A%95%E4%BF%A1%E3%81%93%E3%81%AE8%E6%9C%AC-%E4%B8%AD%E9%87%8E-%E6%99%B4%E5%95%93/dp/4534056877″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”stdO3″});
まとめ
投資初期では良好な成績を収めていた株式が、一転大きく毀損しており、特定の資産クラスに資金を集中させることの恐ろしさを実感します。
投資信託は手軽に分散投資が行える優れた金融商品ですが、市場全体の変動にはどうしてもつられてしまいます。
そんな状況であっても、異なる変動性を持つ別の資産クラスに広く投資することで、資産全体の変動性を抑えることが可能です。
複数の資産クラスに分散することをアセット・アロケーション(資産配分)といいますが、投資成果の大部分はこのアセット・アロケーションによって決まるとも言われています。
アセット・アロケーションの重要性は以下の書籍でも強調されています。
(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”お金は寝かせて増やしなさい”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51xHIGALUZL.jpg”,”/51UFsW4HuvL.jpg”,”/51d7m7hcbYL.jpg”,”/61ULYpbutcL.jpg”,”/51uCgEZrhmL.jpg”,”/51ne7%2Bl4ysL.jpg”,”/51TjKtJWpzL.jpg”,”/51Zj-OmTSML.jpg”,”/410JAnn80uL.jpg”,”/51cjtS6tWPL.jpg”,”/61Q0Zvqja7L.jpg”,”/613B004TKQL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%81%8A%E9%87%91%E3%81%AF%E5%AF%9D%E3%81%8B%E3%81%9B%E3%81%A6%E5%A2%97%E3%82%84%E3%81%97%E3%81%AA%E3%81%95%E3%81%84-%E6%B0%B4%E7%80%AC%E3%82%B1%E3%83%B3%E3%82%A4%E3%83%81/dp/4894517833″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″}});
















最近のコメント