こんにちは、毛糸です。
「長期投資は安全」というイメージを抱いていませんか?
全国銀行協会のサイト(リンク)でも、長期投資の安全性に関して以下のように書いてあります。
一時的に価格が下がっても、長い目で見れば価格が上がることもあるため、長く保有すればするほど、リスクを軽減する効果があるといわれています。
しかし、この主張は極めて誤解しやすいもので、実際にはむしろ、投資収益のリスクは長期になればなるほど大きくなります。
本記事では「投資シミュレーションプログラム」を用いて、長期投資がリスクを高めることを証明します。
参考記事:>>「投資シミュレーションプログラム」サマリー
投資の「リスク」の定義
投資におけるリスクとは、投資収益の期待値からのブレを指すのが一般的です。
もう少し踏み込んで言えば、そのブレを測る尺度が、標準偏差や分散という統計量です。
投資において「リスクが高い」とは、将来の(額もしくは率ベースの)投資収益の標準偏差が高い、ということを意味します。
この意味において、投資が長期になればなるほど、リスクは高くなります。
つまり、他の条件を一定とすれば、短期と長期の投資収益は、後者のほうが高い標準偏差を持つということです。
本記事ではこのことを「投資シミュレーションプログラム」を用いて示します。
(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”ウォール街のランダムウォーカー株式投資の不滅の真理”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51j3XxuLcML.jpg”,”/51L5VguO16L.jpg”,”/51pXH1cT26L.jpg”,”/51qzhDA8N8L.jpg”,”/516KF7nD4ML.jpg”,”/51RqxJ5YdzL.jpg”,”/41Z4TQLguaL.jpg”,”/41RDCEkVSWL.jpg”,”/51ZC6wiROQL.jpg”,”/416UAK2gjbL.jpg”,”/51COLQfOYZL.jpg”,”/41wAkIpxalL.jpg”,”/517pu9qvoaL.jpg”,”/51Qd00xstPL.jpg”,”/41a6WwcjPUL.jpg”,”/41whOykxo9L.jpg”,”/51ZYk6jqWTL.jpg”,”/51JXyzvOypL.jpg”,”/51Cx1OLwZwL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%82%A6%E3%82%A9%E3%83%BC%E3%83%AB%E8%A1%97%E3%81%AE%E3%83%A9%E3%83%B3%E3%83%80%E3%83%A0%E3%83%BB%E3%82%A6%E3%82%A9%E3%83%BC%E3%82%AB%E3%83%BC%E3%80%88%E5%8E%9F%E8%91%97%E7%AC%AC11%E7%89%88%E3%80%89-%E2%80%95%E6%A0%AA%E5%BC%8F%E6%8A%95%E8%B3%87%E3%81%AE%E4%B8%8D%E6%BB%85%E3%81%AE%E7%9C%9F%E7%90%86-%E3%83%90%E3%83%BC%E3%83%88%E3%83%B3%E3%83%BB%E3%83%9E%E3%83%AB%E3%82%AD%E3%83%BC%E3%83%AB/dp/4532356873″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”azSuX”});
リンク
投資シミュレーションプログラム
「投資シミュレーションプログラム」は、確率論に基づくモンテカルロ・シミュレーションという手法を用いて、投資収益の将来予測をするプログラムです。
参考記事:>>「投資シミュレーションプログラム」サマリー
モンテカルロ・シミュレーションとは、コンピュータによって乱数を発生させ、将来を確率的にシミュレートし、大数の法則によって将来の期待値を算定する手法です。
「投資シミュレーションプログラム」を使えば、投資の期待リターンとリスクと投資期間を入力することで、将来の資産額を計算することが出来ます。
長期投資でリスクは低減されない
今回行うシミュレーションは、投資対象をFXとした場合(期待リターン0%、リスク10%と仮定)と、インデックス投信に分散投資した場合(期待リターン4.57%、リスク12.8%)の2つのケースについて、1年・10年・30年の各投資期間で、将来時点で確定する投資収益の期待値とリスクを計算してみます。
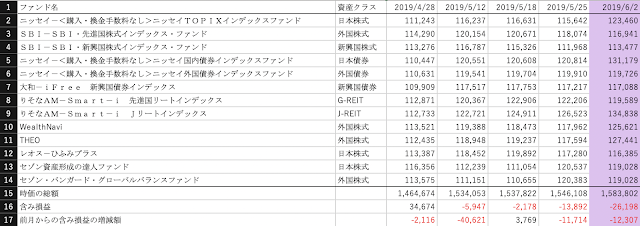
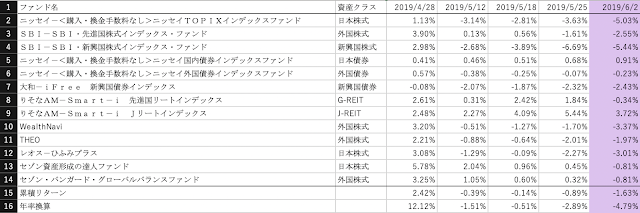
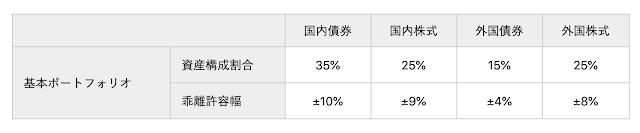
インデックス投信に分散投資、といってもアセット・アロケーションは無限にありますが、ここでは日本の年金運用の基本ポートフォリオと同じ資産配分で行うものと仮定します。
シミュレーション結果は以下のとおりです。
FX(期待リターン0%、リスク10%)に投資した場合
1年後
- リターンの期待値は0%
- リスク(標準偏差)は10%
- シャープレシオは0
- 1年あたりの平均リターンは0%
10年後
- リターンの期待値は0%
- リスク(標準偏差)は32%
- シャープレシオは0
- 1年あたりの平均リターンは0%
30年後
- リターンの期待値は1%
- リスク(標準偏差)は61%
- シャープレシオは0.02
- 1年あたりの平均リターンは0%
FX(期待リターン0%、リスク10%)に投資した場合、長期になってもリターンは(ほぼ)増えませんが、リスクは長期になればなるほど大きくなっていることがわかります。
インデックスに分散投資(期待リターン4.57%、リスク12.8%)した場合
1年後
- リターンの期待値は5%
- リスク(標準偏差)は12%
- シャープレシオは0.4
- 1年あたりの平均リターンは5%
10年後
- リターンの期待値は56%
- リスク(標準偏差)は63%
- シャープレシオは0.8
- 1年あたりの平均リターンは5%
30年後
- リターンの期待値は286%
- リスク(標準偏差)は298%
- シャープレシオは1
- 1年あたりの平均リターンは5%
インデックスに分散投資(期待リターン4.57%、リスク12.8%)した場合、長期になればなるほどリターンは大きくなっていますが、それに伴いリスクも大きくなっていることがわかります。ちなみに、投資のリスクとリターンの比率を示すシャープレシオは、投資が長期化するほど高まります。
上記分析に用いたRのコードは以下のとおりです。
#FX
#投資年数(自由入力)
Year<-1
#シミュレーション回数(自由入力、多いほど正確だが時間がかかる)
sample<-10000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)
#初期投資額を入力(自由入力)
initial<-100
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#期待リターン(期待収益率μ、自由入力)
mu<-0/100
#リスク(標準偏差σ、自由入力)
sigma<-10/100
#シミュレーション開始
set.seed(123)
#sampleの計算は明示せずベクトル化
for ( t in 1:Year){
#今年の資産額=前年の資産額*(1+収益率)
A[,t+1]<-A[,t]*(1+rnorm(sample,mu,sigma))
}
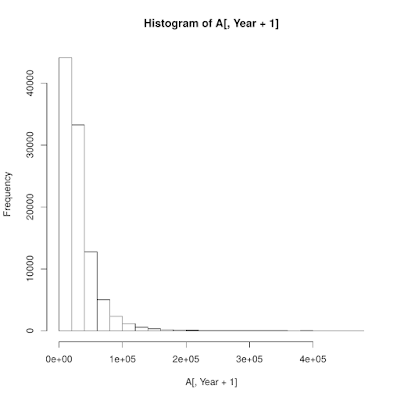
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の平均は",mean(A[,Year+1]),"万円")
paste(Year,"年後の累積リターンの平均は",(mean(A[,Year+1])/initial-1)*100,"%")
paste(Year,"年後の累積リターンの標準偏差は",sd(A[,Year+1])/initial*100,"%")
paste(Year,"年間の1年あたり 平均収益率は",((mean(A[,Year+1])/initial)^(1/Year)-1)*100,"%")
#インデックス
#投資年数(自由入力)
Year<-1
#シミュレーション回数(自由入力、多いほど正確だが時間がかかる)
sample<-10000
#シミュレーション数値を格納する行列
A<-matrix(0,sample,Year+1)
#初期投資額を入力(自由入力)
initial<-100
#シミュレーション数値に初期投資額を入力
A[,1]<-initial
#期待リターン(期待収益率μ、自由入力)
mu<-4.57/100
#リスク(標準偏差σ、自由入力)
sigma<-12.8/100
#シミュレーション開始
set.seed(123)
#sampleの計算は明示せずベクトル化
for ( t in 1:Year){
#今年の資産額=前年の資産額*(1+収益率)
A[,t+1]<-A[,t]*(1+rnorm(sample,mu,sigma))
}
#シミュレーション結果の期待値を表示
paste(Year,"年後の資産額の平均は",mean(A[,Year+1]),"万円")
paste(Year,"年後の累積リターンの平均は",(mean(A[,Year+1])/initial-1)*100,"%")
paste(Year,"年後の累積リターンの標準偏差は",sd(A[,Year+1])/initial*100,"%")
paste(Year,"年間の1年あたり 平均収益率は",((mean(A[,Year+1])/initial)^(1/Year)-1)*100,"%")
考察
FXでもインデックス投資でも、投資が長期になればなるほど、リターンもリスクも大きくなることがわかりました。
本記事の主張を再度述べると、「長期投資をしてもリスクは低くならず、むしろ高まる」ということです。
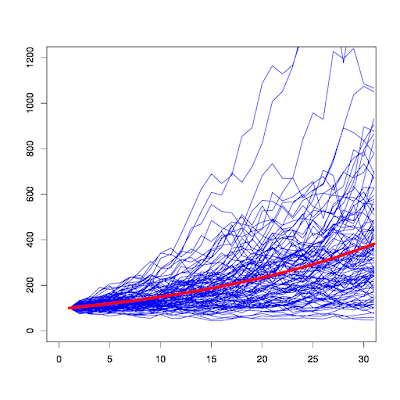
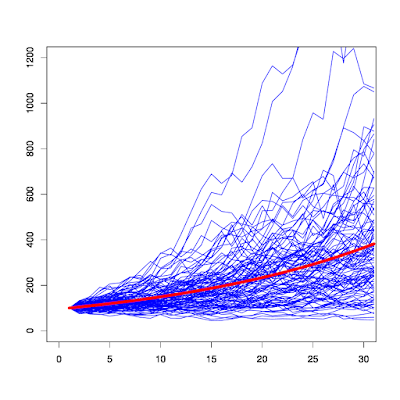
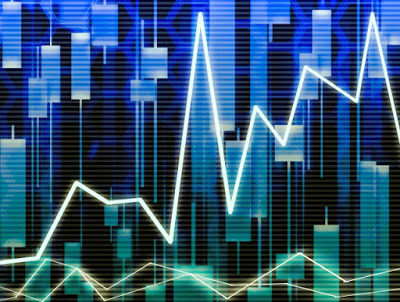
ちなみに、上記インデックス投資のシミュレーションを図示すると以下のようになります。青い線の1つ1つがシミュレートした資産額の変動であり、長期になればなるほど期待値(赤線)からのブレ(リスク)が大きくなっていることがわかります。
まとめ
投資シミュレーションプログラムによる予測の結果、投資期間が長期になるほど、将来時点でのリターンのブレは大きくなることがわかりました。
つまり「長期投資はリスクを低減する」という主張は、リスクを収益率のブレと解釈する限り、正しくありません。
この点に関しては多くの文献で誤解を招く表現がされているので、十分ご注意下さい。
(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”[参考文献]ファイナンスのためのRプログラミング証券投資理論の実践に向けて”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:””,”p”:[“/images/I/41UrHrQ9vlL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%8A%E3%83%B3%E3%82%B9%E3%81%AE%E3%81%9F%E3%82%81%E3%81%AER%E3%83%97%E3%83%AD%E3%82%B0%E3%83%A9%E3%83%9F%E3%83%B3%E3%82%B0-%E2%80%95%E8%A8%BC%E5%88%B8%E6%8A%95%E8%B3%87%E7%90%86%E8%AB%96%E3%81%AE%E5%AE%9F%E8%B7%B5%E3%81%AB%E5%90%91%E3%81%91%E3%81%A6%E2%80%95-%E5%A4%A7%E5%B4%8E-%E7%A7%80%E4%B8%80/dp/4320110447″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”GI2A5″});
リンク












最近のコメント