こんにちは、毛糸です。
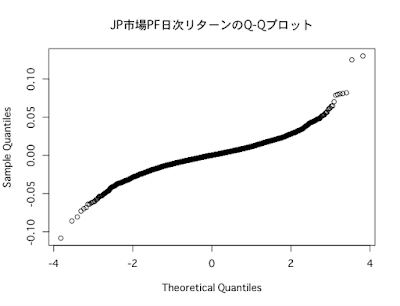
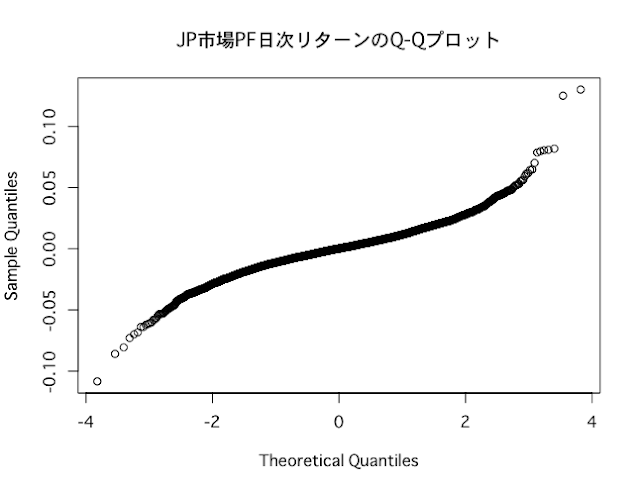
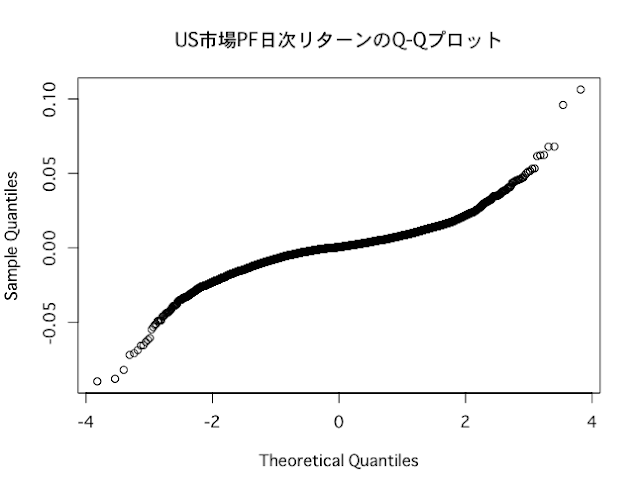
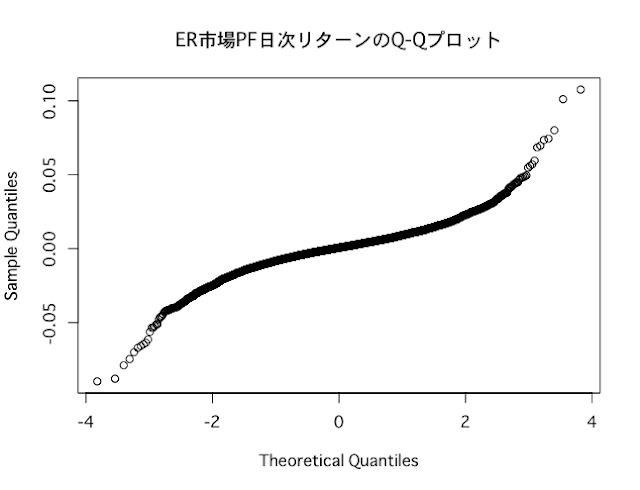
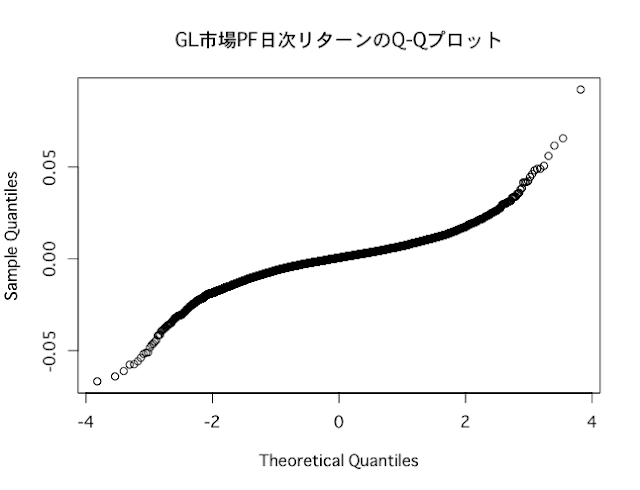
先日の記事で、主要な株価指数から計算する日次リターンが、正規分布に従わないことを確かめました。
>>日本株式、米国株式、欧州株式、全世界株式の日次リターンが正規分布ではなかった件
この記事を見て「ファイナンス理論は嘘だった!」と受け取る方もいたようです。
しかし、このような態度は学術的に価値あるものではないように思います。
本記事では「リターンは正規分布でない」とわかったあとに我々が考えるべきことは何か、ファイナンスの数理モデルにおいて正規分布を仮定していたのにはどういう意味があったのかということについて考えてみたいと思います。
正規分布の仮定と現実の分布の差異
ファイナンス理論ではしばしば、資産価格のリターンは正規分布に従うと仮定されます。
分散投資の理論的根拠とも言われるマーコウィッツの平均分散分析や、シャープらのCAPM(資本資産価格モデル)も、リターンが正規分布に従うときに成り立つ命題です。
また、ファイナンスの数理分析が広がる契機となったブラック・ショールズモデルも、資産の瞬間的な収益率が正規分布に従うという性質を持ちます。
マートンの最適ポートフォリオ理論も、ブラック・ショールズモデルと同様、瞬間的な収益率が正規分布に従うような資産を考えるときにエレガントな結果が得られることがわかっています。
このように、「リターンが正規分布に従う」というのは、教科書的なファイナンスの世界ではスタンダードな仮定であり、その前提を基に膨大な研究成果が蓄積されています。
ところが、下記記事で分析している通り、主要な株価指数の日次リターンは、正規分布に従っていません。
>>日本株式、米国株式、欧州株式、全世界株式の日次リターンが正規分布ではなかった件
理論の前提が現実を捉えきれていないというこの状況を「理論の敗北」と捉える人もいるでしょう。
しかし、そういった考え方は果たして適切なのでしょうか。
数理モデルを考える意味とは
この世の現象を完全に説明できる「万能の理論」などというものはありません。
縮尺1:1の地図は役に立たない
というのは、数理モデルを扱うを行う人がよく使う格言ですが、現実を捨象し分析に関係ある部分を抽象化して考える「モデル分析」を行う場合には、どうしても現実と不整合な部分が出てこざるを得ません。
ファイナンスにおける正規分布の仮定も、こうした「抽象化」の産物です。
つまり、現実にはリターンが正規分布に従っていないことはわかっているけれども、ファイナンスにおいて重要な意味をもつ「リスク」に関する洞察が得られやすく、数学的にも扱いやすいため、正規分布を仮定しているのだということです。
分析したい対象によって、捨象すべき部分は思い切って捨て去る、そうすることでシャープな結論が得られ、世界を理解することにつながります。
リターンが正規分布に従わないという現実はたしかにありますが、リターンの分布という特徴を敢えて捨象することで、ファイナンスは多くの発見を生み出してきたということです。
理論の前提が現実とが整合していなくとも、分析対象について良い考察が得られれば価値がある。
これが科学的態度です。
理論が現実と違うとわかった私たちが、このあと考えるべきこと
リターンの正規性という理論の前提は、現実には成り立っていない。
それを知った私たちは、その後どんな態度をとるべきでしょうか。
間違っても「理論の前提がおかしい!既存理論は無意味だった!」と吹聴してはいけません。
理論はあくまで分析に必要なもののみをすくい取り、関係ない部分を捨象しているので、モデルと現実が乖離するのは当たり前です。
悲しいことに、投資家の間では、過去何度も、こうした建設的でない批判が繰り返されてきたようです。
参考記事>>分散投資を批判した後の対案がそれ以上に酷い法則-梅屋敷商店街のランダム・ウォーカー(インデックス投資実践記)
現実とモデルが違うなんてことはみんなわかっていて、わかっていてなお有用だから、使われているわけです。
理論と現実の差異に気づいたあとに取るべきスタンスは
- 理論と現実の差を受け入れ、単純化した世界(モデル)で成り立つ命題を受け入れる
- 理論と現実の差を埋めるような、新たな手法やモデルを開発する
もし標準的なモデルが自分の分析において不都合なら、自分に必要なモデルを自分で作ればいいだけの話です。
(function(b,c,f,g,a,d,e){b.MoshimoAffiliateObject=a;
b[a]=b[a]||function(){arguments.currentScript=c.currentScript
||c.scripts[c.scripts.length-2];(b[a].q=b[a].q||[]).push(arguments)};
c.getElementById(a)||(d=c.createElement(f),d.src=g,
d.id=a,e=c.getElementsByTagName(“body”)[0],e.appendChild(d))})
(window,document,”script”,”//dn.msmstatic.com/site/cardlink/bundle.js”,”msmaflink”);
msmaflink({“n”:”金融経済学の基礎 (ファイナンス講座)”,”b”:””,”t”:””,”d”:”https://images-fe.ssl-images-amazon.com”,”c_p”:”/images/I”,”p”:[“/51j7faeOtGL.jpg”,”/51j7faeOtGL.jpg”],”u”:{“u”:”https://www.amazon.co.jp/%E9%87%91%E8%9E%8D%E7%B5%8C%E6%B8%88%E5%AD%A6%E3%81%AE%E5%9F%BA%E7%A4%8E-%E3%83%95%E3%82%A1%E3%82%A4%E3%83%8A%E3%83%B3%E3%82%B9%E8%AC%9B%E5%BA%A7-%E6%B1%A0%E7%94%B0-%E6%98%8C%E5%B9%B8/dp/4254545525″,”t”:”amazon”,”r_v”:””},”aid”:{“amazon”:”1251300″,”rakuten”:”1249750″,”yahoo”:”1251299″},”eid”:”JJh4M”});
まとめ
しかしこれは「理論の敗北」ではありません。
理論は、現実の問題の本質的な部分を抽象化して取り出し、その他の部分はきっぱり単純化することで、深い洞察を得ており、「リターンが正規分布に従う」という仮定も、こうした単純化の一環です。
理論と現実が異なっていると気づいたなら、その差異を受け入れるか、より現実的なモデルを自分で作ってみるのが、社会的に意義ある態度です。















最近のコメント