こんにちは、毛糸です。
先日こんなつぶやきをしました。
「京都大学がビッグデータの新統計法則を発見、「べき則」の普遍性を解明」というニュースを読んで – アドレナリン https://t.co/yNN0PtTu6i安定分布について調べていたら、京大研究者による「超一般化中心極限定理」に行き着いたのだけど、どうも証明が怪しいらしい。
— 毛糸 (@keito_oz) July 25, 2019
本記事では株価リターンを題材に、確率論における中心極限定理とその一般化についてまとめます。
中心極限定理とその一般化
「独立同分布の確率変数の和は正規分布に従う」というのが中心極限定理のざっくりとした内容です。
中心極限定理は確率論における重要な定理であり、それが成立するための前提条件がもちろんあります。
ある定理を、より広い範囲に適用できるようにしたり、前提条件を緩めたりした場合にも成り立つことを示す、というのは、数学においてはよく行われます。
こうした「一般化」は中心極限定理についても存在し、一般化中心極限定理という「拡張版の中心極限定理」では、確率変数の和は正規分布ではなく、べき乗則をもつ安定分布に従うことが示されます。
正規分布に従わない株価リターン
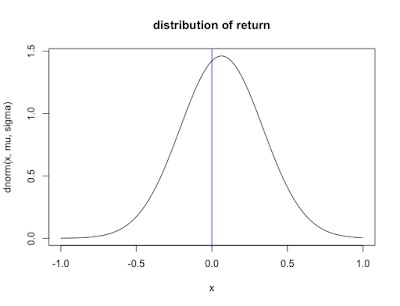
株式リターンの実際の分布は、正規分布よりも「レアな値が出やすい」ものであり、統計的には正規分布に従いません。
【参考記事】
日本株式、米国株式、欧州株式、全世界株式の日次リターンが正規分布ではなかった件
ファイナンスの多くの理論では、リターンの正規性を仮定して結論を導いていますから、実際のリターンが正規分布ではないことについて危機感を覚える人もいるでしょう。
しかし実は正規分布でないケースにも、多くの理論は成り立ちます。
【参考記事】
株価リターンが正規分布でなくてもファイナンス理論は成り立ちます!
べき乗則と一般化中心極限定理
正規分布でなければ何なのだ、ということで注目されているのが、「べき乗則」を持つ分布です。
リターンが正規分布に従うとき、「レアな」リターンが実現する確率は、期待リターンから遠くなればなるほど急激に減っていきます。
しかし実際には、「レアな」リターンはそれほど急激に減っていくものではなく、「べき乗則」というゆったりとした減り方をしているという研究があります。
一般化中心極限定理の帰結として得られる安定分布はこのべき乗則に則った確率分布であり、実際の金融データへの当てはまりの良さが期待されています。
冒頭で述べた超一般化中心極限定理は、これを更に広範囲に拡張した定理のようです。









最近のコメント